Giáo viên cần chọn ra 2 nhóm từ 10 nhóm để đánh giá học tập của các nhóm còn lại. Tính xác suất của biến cố: "Chọn ra nhóm 1,2 hoặc 3,4 đánh giá các nhóm còn lại"
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài học: Muốn biết chính xác kết quả, ta nên đo đạc chính xác kết hợp tính toán

- Kết quả 1: Chọn 2 nhóm: A và B rồi sắp xếp thứ tự “ A trình bày trước, B trình bày sau” hoặc “ B trình bày trước, A trình bày sau”.
- Kết quả 2: Chọn 2 nhóm: A và C rồi sắp xếp thứ tự “ A trình bày trước, C trình bày sau” hoặc “ C trình bày trước, A trình bày sau”.
- Kết quả 3: Chọn 2 nhóm: A và D rồi sắp xếp thứ tự “ A trình bày trước, D trình bày sau” hoặc “ D trình bày trước, A trình bày sau”.
- Kết quả 4: Chọn 2 nhóm: B trình bày và C trình bày rồi sắp xếp thứ tự “ B trình bày trước, C trình bày sau” hoặc “ C trình bày trước, B trình bày sau”.

- Học sinh 1: (đề số 1) 2(x -2) + 1 = x - 1
⇔ 2x – 4 – 1 = x -1 ⇔ x = 2
- Học sinh 2: (đề số 2) Thay x = 2 vào phương trình ta được:
(2 + 3)y = 2 + y ⇔ 5y = 2 + y ⇔ y = 1/2
- Học sinh 3: (đề số 3) Thay y = 1/2 vào phương trình ta được:
- Học sinh 4 (đề số 4) thay z = 2/3 vào phương trình ta được:
Vậy t = 2.

- Tên nhóm nghề:
+ Nghề muốn chọn nhất: Cảnh sát.
+ Nghề muốn chọn nhì: Giáo viên.
+ Nghề muốn chọn 3: Hướng dẫn viên du lịch.
- Những đặc điểm của bản thân, bao gồm sở thích, khả năng, tính cách, điểm mạnh, điểm yếu.
+ Sở thích: Thích giao lưu làm những điều tốt cống hiến cho xã hội, thích đi du lịch.
+ Tính cách: Có phần hơi nóng nảy, hòa đồng.
+ Điểm mạnh: Quan tâm chăm sóc giúp đỡ mọi người xung quanh.
+ Điểm yếu: Nóng tính, đôi khi còn rụt rè.
- Đối chiếu đặc điểm của bản thân với đặc điểm của nhóm nghề để đánh giá sự phù hợp của bản thân với nhóm nghề để đánh giá sự phù hợp của bản thân với nhóm nghề định lựa chọn.

Đáp án B
Gọi x,y lần lượt là số học sinh nữ ở nhóm I và nhóm II. Khi đó số học sinh nam ở nhóm II là 25 − 9 + x − y = 16 − x − y . Điều kiện để mỗi nhóm đều có học sinh nam và nữ là x ≥ 1, y ≥ 1,16 − x − y ≥ 1 ; x , y ∈ ℕ .
Xác suất để chọn ra được hai học sinh nam bằng C 9 1 C 16 − x − y 1 C 9 + x 1 C 16 − x 1 = 0,54
⇔ 9 16 − x − y 9 + x 16 − x = 0,54 ⇔ 144 − 9 x − 9 y 144 + 7 x − x 2 = 0,54 ⇔ y = 184 25 − 71 50 x + 3 50 x 2
Ta có hệ điều kiện sau x ≥ 1 184 25 − 71 50 x + 3 50 x 2 ≥ 1 16 − x − 184 25 − 71 50 x + 3 50 x 2 ≥ 1 x ∈ ℕ
⇔ x ≥ 1 3 50 x 2 − 71 50 x + 159 25 ≥ 0 − 3 50 x 2 + 21 50 x + 191 25 ≥ 0 x ∈ ℕ ⇔ x ≥ 1 x ≥ 53 3 x ≤ 6 21 − 5 201 6 ≤ x ≤ 21 + 5 201 6 x ∈ ℕ ⇔ 1 ≤ x ≤ 6 x ∈ ℕ
Ta có bảng các giá trị của :
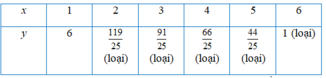
Vậy ta tìm được hai cặp nghiệm nguyên x ; y thỏa mãn điều kiện là 1 ; 6 và 6 ; 1 .
Xác suất để chọn ra hai học sinh nữ là C x 1 C y 1 C 9 + x 1 C 16 − x 1 = x y 9 + x 16 − x .
Nếu x ; y ∈ 1 ; 6 , 6 ; 1 thì xác suất này bằng 1 25 = 0,04 .

Tổng số khả năng có thể xảy ra của phép thử là \(n\left( \Omega \right) = C_{12}^4\)
a) Số kết quả thuận lợi cho biến cố “Bốn bạn thuộc 4 tổ khác nhau” là số cách sắp xếp 4 bạn vào 4 tổ có \(4!\) cách
Vậy xác suất của biến cố “Bốn bạn thuộc 4 tổ khác nhau” là \(P = \frac{{4!}}{{C_{12}^4}} = \frac{8}{{165}}\)
b) Gọi A là biến cố “Bốn bạn thuộc 2 tổ khác nhau”
A xảy ra với 2 trường hợp sau:
TH1: 3 bạn cùng thuộc 1 tổ và 1 bạn thuộc tổ khác có \(C_4^3.C_3^1.C_2^1 = 24\) cách
TH2: cứ 2 bạn cùng thuộc 1 tổ \(C_4^2.C_3^1.C_2^2.C_2^1 = 36\) cách
Suy ra, số kết quả thuận lợi cho biến cố A là \(n\left( A \right) = 24 + 36 = 60\)
Vậy xác suất của biến cố “Bốn bạn thuộc 2 tổ khác nhau” là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{60}}{{C_{12}^4}} = \frac{4}{{33}}\)


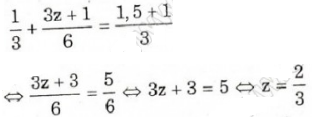
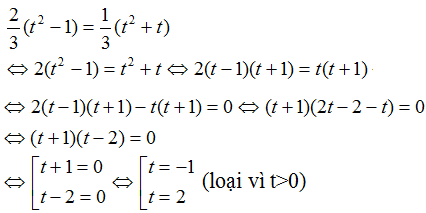

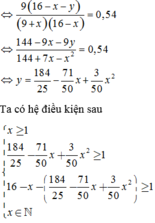
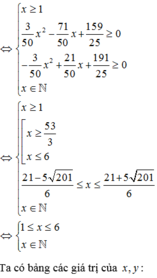



Có \(C_{10}^2\) cách chọn 2 nhóm bất kì (không gian mẫu)
Có 2 biến cố thuận lợi: 1,2 hoặc 3,4
Do đó xác suất là: \(P=\dfrac{2}{C_{10}^2}\)
Ngồi học em nghĩ ra cái đề này anh ạ!