Cho tam giác ABC có góc A = 90o. M là trung điểm BC. Cm : AM = \(\frac{BC}{2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TD
7 tháng 3 2016
M là trung điểm=> BC=AM.2= 2.2= 4cm
Nếu MAB vuông=> AC là cạnh huyền. Có:
AB^2 + BC^2= AC^2
3^2+4^2= 25= 5^2
=> AC=5
=> MAB=90o
tick cho mk nha!
TD
29 tháng 12 2021
HAI TAM GIÁC BẰNG NHAU NÊN 2 GÓC BẰNG HAU CÒN CÂU 2 THÌ MINK CHX BIẾT
20 tháng 11 2023
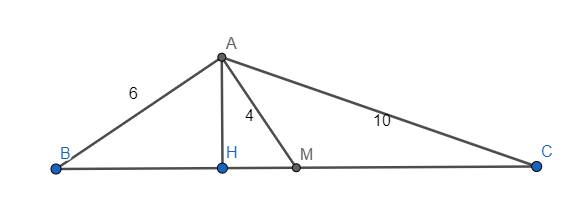
Hạ \(AH\perp BC\) tại H. Đặt \(MB=MC=x;HM=y;AH=h\)
Theo định lý Pythagoras: \(\left\{{}\begin{matrix}AH^2+HM^2=AM^2\\AH^2+BH^2=AB^2\\AH^2+CH^2=AC^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}h^2+y^2=16\\h^2+\left(x-y\right)^2=36\\h^2+\left(x+y\right)^2=100\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}h^2+y^2=16\\h^2+x^2+y^2-2xy=36\\h^2+x^2+y^2+2xy=100\end{matrix}\right.\)
Cộng theo vế của 2 pt thứ 2 và thứ 3 của hệ này, ta được:
\(2\left(h^2+x^2+y^2\right)=136\)
\(\Leftrightarrow x^2+\left(h^2+y^2\right)=68\)
\(\Leftrightarrow x^2+16=68\)
\(\Leftrightarrow x^2=52\) hay \(BM^2=52\)
Mà ta lại có \(AB^2+AM^2=6^2+4^2=52\)
\(\Rightarrow AB^2+AM^2=BM^2\) \(\Rightarrow\Delta ABM\) vuông tại A \(\Rightarrow\) đpcm
MH
20 tháng 11 2023
Gọi H là điểm đối xứng với A qua M
Xét tam giác AMB và tam giác HMC có:
\(\left\{{}\begin{matrix}HM=AM\\\widehat{AMB}=\widehat{HMC}\\MB=MC\end{matrix}\right.\)
\(\Rightarrow\Delta AMB=\Delta HMC\left(c.g.c\right)\)
\(\Rightarrow HC=AB=6cm\)
Xét tam giác HAC có:
\(AH^2+HC^2=10^2\left(8^2+6^2=10^2\right)\)
\(\Rightarrow\widehat{AHC}=90^o\)
Mà \(\Delta AMB=\Delta HMC\)
\(\Rightarrow\widehat{MAB}=\widehat{MHC}=90^o\left(đpcm\right)\)
S
21 tháng 2 2019
tự kẻ hình :
a, tam giác ABM và tam giác ACM có : AB =AC (gt)
AB = AC => tam giác ABC cân => góc B = góc C
AM = MC do ...
=> tam giác ABM = tam giác ACM
21 tháng 2 2019
Bạn tự vẽ hình ra nka. Mình chỉ c/m thôi.
a. Tam giác ABC có AB = AC ( gt )
=> Tam giác ABC cân tại A
=> góc ABC = góc BAC ( hai góc ở đáy )
Xét tam giác ABM và tam giác ACM có:
AB = AC < gt >
góc ABC = góc ACB ( cmt )
AM chung
=> tam giác ABM = tam giác ACM < c.g.c>
=> góc BAM = góc ACM ( hai góc tương ứng )
=> AM là tia phân giác của góc BAC < đpcm >
b. Tam giác ABM bằng tam giác ACM < cmt >
=> góc AMB bằng góc AMC < hai góc t/ư > <1>
Mà có góc AMB + góc AMC bằng 180 độ < kề bù > <2>
Từ <1> và <2> -> góc AMB bằng 90 độ
-> AM vuông góc BC < đpcm>
Học tốt nekkk. k cho mina nka <3.
Gợi ý nhé, trên tia đối tia MA lấy điểm H/ MA=MH
Nếu bạn cần cách giải thì bảo mình nhé, nhớ tick đúngcho mik nha ^^
ko mik cần lời giải cơ
mik mới lớp 6 lên 7 thôi biết gì mấy định lí