Cho đường tròn tâm $O$ bán kính $R$ và một điểm $A$ nằm ngoài đường tròn. Kẻ một đường thẳng đi qua $A$ và không đi qua $O$, cắt đường tròn tại hai điểm phân biệt $M$, $N$ ($M$ nằm giữa $A$ và $N$). Từ $A$ vẽ hai tiếp tuyến $AB$ và $AC$ với $(O)$ ($B$, $C$ là hai tiếp điểm). Đường thẳng $BC$ cắt $AO$ tại $H$. Gọi $I$ là trung điểm của $MN$. Đường thẳng $OI$ cắt đường thẳng $BC$ tại $E$. Chứng minh $AHIE$ là tứ giác nội tiếp.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ACB=1/2*sđ cung AB=90 độ
=>ΔACN vuông cân tại C
góc ACN+góc AMN=180 độ
=>AMNC nội tiếp
b: AMNC nội tiếp
=>góc CNA=góc CMA=góc BMD
góc BNE=1/2(sđ cung BE-sđ cung AC)
góc DMB=1/2*(sđ cung BD-sđ cung AC)
=>sđ cung BD=sđ cung BE
=>B nằm trên trung trực của DE
Xét ΔADB và ΔAEB có
góc ADB=góc aEB
AB chung
DB=BE
=>ΔABD=ΔAEB
=>AD=AE
=>A nằm trên trung trực của DE
=>AB là trung trực của DE
=>DE vuông góc AB

1: ΔOAB cân tại O
mà OI là trung tuyến
nên OI vuông góc AB
góc OIM=góc OCM=góc ODM=90 độ
=>O,I,M,D,C cùng thuộc đường tròn đường kính OM
góc DIM=góc MOD
góc CIM=góc COM
mà góc COM=góc DOM
nên góc DIM=góc CIM
=>IM là phân giác của góc CID

a, Ta có SA = SB (tc tiếp tuyến cắt nhau )
OA = OB = R
Vậy OS là đường trung trực đoạn AB
=> SO vuông AB tại H
b, Vì I là trung điểm
=> OI vuông NS
Xét tứ giác IHSE ta có ^EHS = ^EIS = 900
mà 2 góc này kề, cùng nhìn cạnh ES
Vậy tứ giác IHSE nt 1 đường tròn
=> ^ESH = ^HIO ( góc ngoài đỉnh I )
Xét tam giác OIH và tam giác OSE có
^HIO = ^OSE (cmt)
^O_ chung
Vậy tam giác OIH ~ tam giác OSE (g.g)
\(\dfrac{OI}{OS}=\dfrac{OH}{OE}\Rightarrow OI.OE=OH.OS\)
Xét tam giác OAS vuông tại A ( do SA là tiếp tuyến với A là tiếp điểm), đường cao AH ta có
\(OA^2=OH.OS\)(hệ thức lượng)
\(\Rightarrow OA^2=R^2=OI.OE\)

a) Trong (O) có AB là dây cung không đi qua O và I là trung điểm AB
\(\Rightarrow OI\bot AB\Rightarrow\angle MIO=90\Rightarrow\angle MIO+\angle MCO=90+90=180\)
\(\Rightarrow MIOC\) nội tiếp
b) Vì MC,MD là tiếp tuyến \(\Rightarrow\Delta MCD\) cân tại M có MO là phân giác \(\angle CMD\) \(\Rightarrow MO\bot CD\) mà \(EF\parallel CD\) \(\Rightarrow EF\bot MO\)
tam giác MOE vuông tại O có đường cao OC \(\Rightarrow CM.CE=OC^2\)
tam giác MOC vuông tại C có đường cao HC \(\Rightarrow OH.OM=OC^2\)
\(\Rightarrow OH.OM=CM.CE\)
Vì H là trung điểm CD (\(\Delta MCD\) cân tại M) và \(EF\parallel CD\)
\(\Rightarrow O\) là trung điểm EF
\(\Rightarrow S_{MEF}=2S_{MOE}=2.\dfrac{1}{2}.OC.ME=OC.\left(CM+CE\right)\)
\(\ge R.\sqrt{CM.CE}=R.2\sqrt{OC^2}=R.2OC=2R^2\)
\(\Rightarrow S_{MEF_{min}}=2R^2\) khi \(CM=CE=R\left(CM.CE=R^2\right)\)
\(\Rightarrow OM=\sqrt{R^2+R^2}=\sqrt{2}R\)
Vậy M nằm trên d sao cho \(OM=\sqrt{2}R\) thì diện tích tam giác MEF nhỏ nhất \(\left(=2R^2\right)\)

a: góc OAM+góc OBM=180 độ
=>OAMB nội tiếp
b: Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA/MD=MC/MA
=>MA^2=MD*MC


Ta có
\(AB=AC\) (Hai tiếp tuyến cùng xp từ 1 điểm thì khoảng cách từ điểm đó đến hai tiếp điểm bằng nhau)
\(\Rightarrow\Delta ABC\) cân tại A (1)
AO là phân giác của \(\widehat{BAC}\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường nối điểm đó với tâm của đường tròn là phân iacs của góc tạo bởi 2 tiếp tuyến) (2)
Từ (1) và (2) \(\Rightarrow AH\perp BC\) (Trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường cao, đường trung trực...)
\(\Rightarrow\widehat{AHE}=90^o\) (*)
Ta có
\(OM=ON\) (Bán kính (O)) \(\Rightarrow\Delta OMN\) cân tại O
Ta có \(IM=IN\) (Giả thiết) => ON là đường trung tuyến của tg OMN
\(\Rightarrow OE\perp AN\) (Trong tg cân đường trung tuyến xuất phát từ đỉnh tg cân đồng thời là đường cao, đường trung trực...)
\(\Rightarrow\widehat{AIE}=90^o\) (**)
Từ (*) và (**) => I và H cùng nhìn AE dưới hai góc bằng nhau và bằng 90 độ => I và H nằm trên đường tròn đường kính AE nên 4 điểm A;H;I;E cùng nằm trên 1 đường tròn
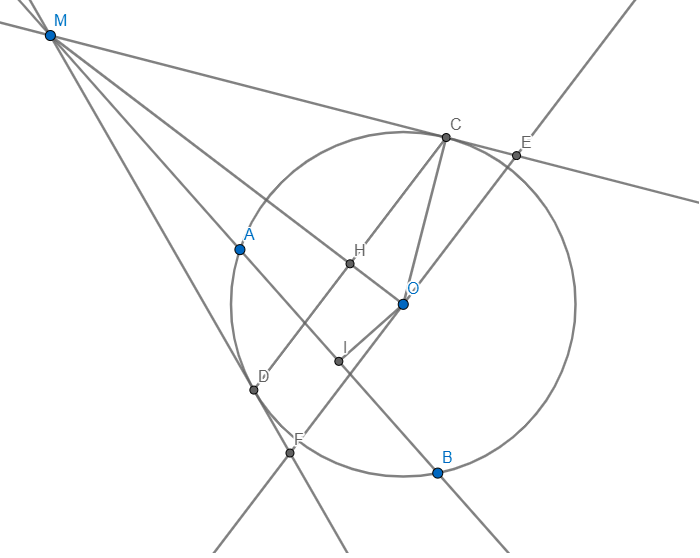
Cho đường tròn tâm OO bán kính RR và một điểm AA nằm ngoài đường tròn. Kẻ một đường thẳng đi qua AA và không đi qua OO, cắt đường tròn tại hai điểm phân biệt MM, NN (MM nằm giữa AA và NN). Từ AA vẽ hai tiếp tuyến ABAB và ACAC với (O)(O) (BB, CC là hai tiếp điểm). Đường thẳng BCBC cắt AOAO tại HH. Gọi II là trung điểm của MNMN. Đường thẳng OIOI cắt đường thẳng BCBC tại EE. Chứng minh AHIEAHIE là tứ giác nội tiếp.
theo gt, ta co:
I là trung điểm của MNMN va MN la day cung cua (O)
=> OE vuong goc voi MN tai I
hay goc AIE= 90 (1)
Mat khac, ta lai co A nam ngoai (O);
AC va AB lan luot la cac tiep tuyen cua (O)
=> AO vuong goc voi BC
hay goc AHE = 90 (2)
tu (1) va (2) => tu giac AHIE noi tiep (vi co 2 goc ke bang nhau)