Cho đường tròn (O:R). Một đường thẳng d không đi qua tâm, cắt đường tròn tại hai điểm A và B phân biệt. Trên d lấy M sao cho A nằm giữa M và B. Từ M kẻ 2 tiếp tuyến MC và MD cới đường tròn ( C và D là 2 tiếp điểm).
a) CMR: MCOD nội tiếp.
b) Gọi I là trung điểm của Ab, đường thẳng IO cắt tia MD tại K. CMR: KD.KM = KI.KO.
c) Một đường thẳng đi qua O và song song với CD, cắt các tia MC và MD lần lượt tại E và F. Xác định vị trí của M trên d sao cho diện tích tam giác MÈ đạt GTNN. Mọi người giải giúp mình câu c với, xin cảm ơn!

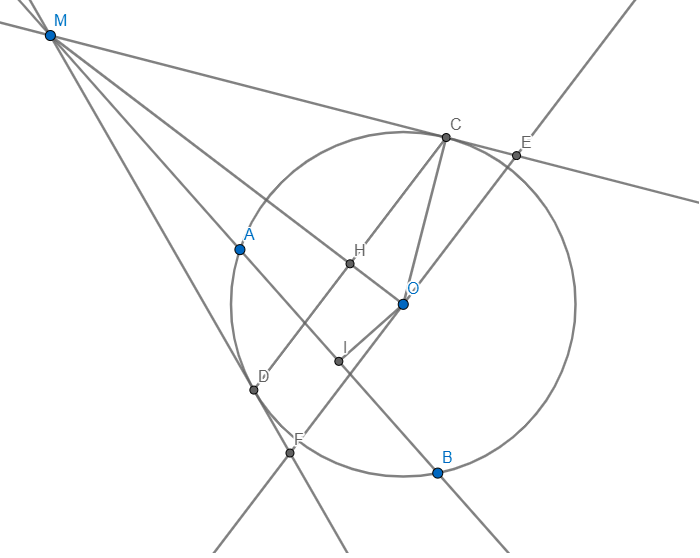


a) Xét tứ giác MCOD có
\(\widehat{MDO}\) và \(\widehat{MCO}\) là hai góc đối
\(\widehat{MDO}+\widehat{MCO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MCOD là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)