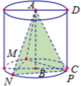
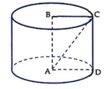
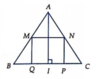
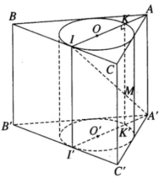
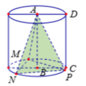
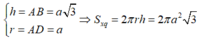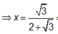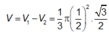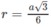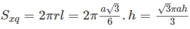Quay hình chữ nhật ABCD quanh trục AB cố định, đường gấp khúc ADBC cho ta hình trụ (T). Gọi Δ M N P là tam giác đều nội tiếp đường tròn đáy (không chứa điểm A). Tính tỷ số giữa thể tích khối trụ và thể tích khối chóp A.MNP.
A. 4 3 3 π .
B. 4 3 π .
C. 3 4 π .
D. 4 3 π .