Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
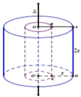
Ta có r 1 = O B = A O − A B = a − x
là bán kính đáy của khối trụ nhỏ.
Và r 2 = O A = a là bán kính đáy của
khối trụ lớn với chiều cao h = 2x
Suy ra thể tích cần tính là
V = V t l − V t n = π r 2 2 h − π r 1 2 h = 2 π x a 2 − a − x 2 = 2 π x 2 a x − x 2 ⇒ V = 2 π x 2 2 a − x = 8 π . x 2 . x 2 . 2 a − x ≤ 8 π . 8 a 3 27 = 64 π a 3 27 ⇒ V max = 64 π a 3 27 .

Đáp án A
Phương pháp: Công thức tính thể tích khối trụ là V = π r 2 h .Trong đó h là chiều cao của hình trụ, r là bán kính đáy.
Cách giải: Ta có: chiều cao h của khối trụ là AD hoặc BC nên h = 2
Bán kính đáy là r = A B 2 = 1 2
Khi đó ta có thể tích khối trụ cần tìm là V = π r 2 h = π . 1 4 .2 = π 2

Đáp án A
Gọi V là thể tích của khối tròn xoay cần tính, khi đó V = V 1 − V 2 với
V1 là thể tích khối trụ có chiều cao h 1 = A B , bán kính R = A D → V 1 = π R 2 h 1 = 2 π a 3
V 2 là thể tích khối trụ có chiều cao h 1 = A B − C D , bán kính R = A D → V 2 = 1 3 π r 2 h 2 = π a 3 3
Vậy thể tích cần tính là V = V 1 − V 2 = 2 π a 3 − π a 3 3 = 5 π a 3 3

Đáp án C
Khối trụ tạo thành có bán kính đáy R = A D 2 = 1 ; và chiều cao h = A B = 1. Vậy thể tích khối trụ cần tính là V = π R 2 h = π .1 2 .1 = π .

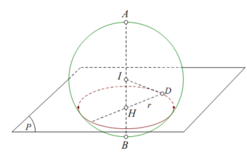
∆ B C D vuông tại C có:
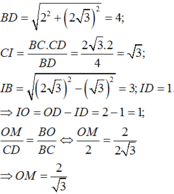
Thể tích khối nón có đỉnh B và đáy là hình tròn tâm I bán kính IC bằng thể tích khối nón có đỉnh D và đáy là hình tròn tâm J bán kính JA bằng:
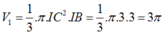
Thể tích khối nón cụt có hai đáy là hình tròn tâm I bán kính IC, hình tròn tâm O bán kính OM bằng thể tích khối nón cụt có hai đáy là hình tròn tâm J bán kính JA, hình tròn tâm O bán kính OM bằng:
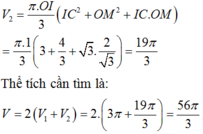
Chọn D.