Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Thể tích khối tròn xoay cần tính là
V = π ∫ 0 π sin 2 2 x d x = π ∫ 0 π 1 − cos 4 x 2 d x = π 2 x − 1 4 sin 4 x 0 π = π 2 π − 0 = π 2 2 .

Đáp án A
Phương pháp: Công thức tính thể tích khối trụ là V = π r 2 h .Trong đó h là chiều cao của hình trụ, r là bán kính đáy.
Cách giải: Ta có: chiều cao h của khối trụ là AD hoặc BC nên h = 2
Bán kính đáy là r = A B 2 = 1 2
Khi đó ta có thể tích khối trụ cần tìm là V = π r 2 h = π . 1 4 .2 = π 2

Theo công thức ta có:
Sxq = 2πrh = 2√3 πr2
Stp = 2πrh + 2πr2 = 2√3 πr2 + 2 πr2 = 2(√3 + 1)πr2 ( đơn vị thể tích)
b) Vtrụ = πR2h = √3 π r3
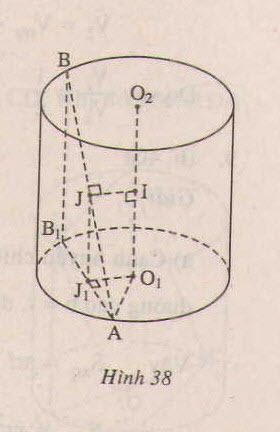
c) Giả sử trục của hình trụ là O1O2 và A nằm trên đường tròn tâm O1, B nằm trên đường tròn tâm O2; I là trung điểm của O1O2, J là trung điểm cảu AB. Khi đó IJ là đường vuông góc chung của O1O2 và AB. Hạ BB1 vuông góc với đáy, J1 là hình chiếu vuông góc của J xuống đáy.
Ta có là trung điểm của
,
= IJ.
Theo giả thiết = 300.
do vậy: AB1 = BB1.tan 300 = = r.
Xét tam giác vuông
AB1 = BB1.tan 300 = O1J1A vuông tại J1, ta có: =
-
.
Vậy khoảng cách giữa AB và O1O2 :