Cho hình chóp tứ giác đều S.ABCD có thể tích bằng 4 3 a 3 3 và diện tích xung quanh bằng 8 a 2 .Tính góc α giữa mặt bên của hình chóp với mặt đáy, biết α là một số nguyên.
A. 55°
B. 30°
C. 45°
D. 60°
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi O là tâm của hình vuông ABCD.
Do S.ABCD là hình chóp đều nên SO ⊥ (ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)


Đáp án A
Đặt r = OA, SO = h, SA = SB = SC = l là đường sinh của hình nón.
Gọi I là trung điểm của đoạn AB.
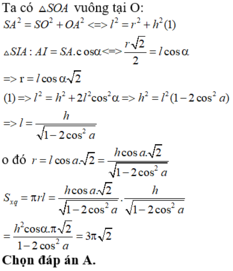

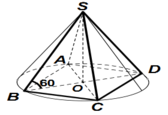
Gọi O là tâm của hình vuông ABCD. Do S.ABCD là hình chóp đều nên SO ⊥(ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)
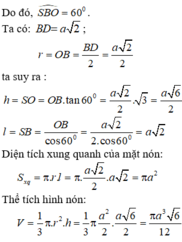

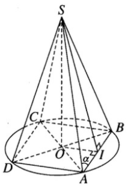
Gọi r là bán kính đáy của hình nón ta có OA = r, SO = h và SA = SB = SC = SD = l là đường sinh của hình nón.
Gọi I là trung điểm của đoạn AB, ta có:
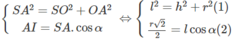
(2) ⇒ r = 2 lcos α
(1) ⇒ l 2 = h 2 + 2 l 2 cos2 α
⇒ h 2 = l 2 (1 − 2cos2 α )
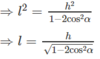
Do đó 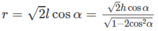
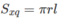
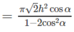

Đề bài thiếu 1 dữ liệu nữa (ví dụ SA vuông góc mặt đáy)
Đáp án là D
+) Gọi độ dài cạnh đáy là x, gọi M là trung điểm của CD, O ≡ AC ∩ BD.
=> ((SCD);( ABCD)) = SMO= α .
+) Theo giả thiết
+) Từ (1) và (2) ta có hệ: