Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
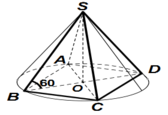
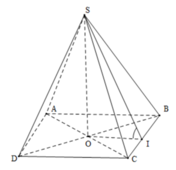
Gọi O là tâm của hình vuông ABCD.
Do S.ABCD là hình chóp đều nên SO ⊥ (ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)


Gọi O là tâm của hình vuông ABCD. Do S.ABCD là hình chóp đều nên SO ⊥(ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)
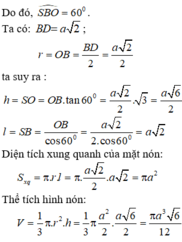

Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
Gọi M là trung điểm AB \(\Rightarrow AB\perp OM\Rightarrow AB\perp\left(SOM\right)\)
\(\Rightarrow\widehat{SMO}\) là góc giữa mặt bên và đáy hay \(\widehat{SMO}=60^0\)
\(SO=OM.tan\widehat{SMO}=\dfrac{a}{2}.tan60^0=\dfrac{a\sqrt{3}}{2}\)
\(V=\dfrac{1}{3}SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}.a^2=\dfrac{a^3\sqrt{3}}{6}\)

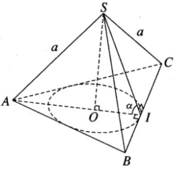
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = SB = SC = a và ∠ SIO = α. Đặt OI = r, SO = h, ta có AO = 2r và

Do đó a 2 = r 2 tan 2 α + 4 r 2 = r 2 tan 2 α + 4
Vậy 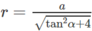
Hình nón nội tiếp có đường sinh là :
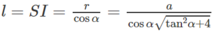
Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:
![]()
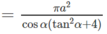

Chọn B.
Gọi H = (AC) ∩ (BD), khi đó S HBA = S SAB . cos 60 °

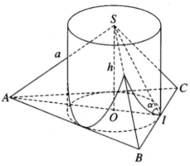
Theo giả thiết ta có tam giác đáy ABC là tam giác đều.
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = a. Đặt OI = r , SO = h , ta có AO = 2r và ∠ SIA = α .
Do đó 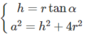
Vậy a 2 = r 2 tan 2 α + 4 r 2 = r 2 tan 2 α + 4
Ta suy ra

Gọi S xq là diện tích xung quanh của hình trụ ta có công thức S xq = 2 π rl trong đó
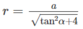
và 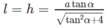
Vậy 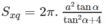
Các mặt bên SAB, SBC , SCA là những phần của ba mặt phẳng không song song với trục và cũng không vuông góc với trục nên chúng cắt mặt phẳng xung quanh của hình trụ theo những cung elip. Các cung này có hình chiếu vuông góc trên mặt phẳng (ABC) tạo nên đường tròn đáy của hình trụ.
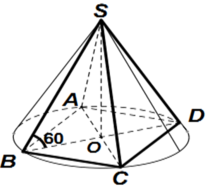
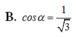
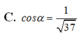
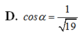
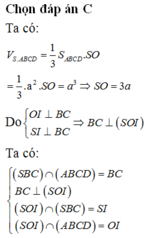
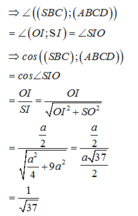
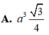
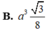

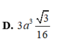

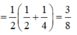

Đáp án là D
+) Gọi độ dài cạnh đáy là x, gọi M là trung điểm của CD, O ≡ AC ∩ BD.
=> ((SCD);( ABCD)) = SMO= α .
+) Theo giả thiết
+) Từ (1) và (2) ta có hệ: