Không sử dụng máy tính, hãy tính: log 3 3 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
10 tháng 12 2019
Đúng(0)
Những câu hỏi liên quan
21 tháng 10 2021
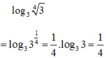
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
H9
HT.Phong (9A5)
CTVHS
18 tháng 8 2023
a) \(log_50,5=-0,439677\)
c) \(In\left(\dfrac{3}{2}\right)=0,405465\)
15 tháng 8 2023
tham khảo
a)Chia cả hai vế của phương trình cho \(2\), ta được:
\(log_2x=-\dfrac{3}{2}\)
Vậy \(log_2x=-\dfrac{3}{2}\)
b) Áp dụng định nghĩa của logarit, ta có:
\(log_2x=-\dfrac{3}{2}\Leftrightarrow2^{-\dfrac{3}{2}}=x\)
Vậy \(x=\dfrac{\sqrt{2}}{4}\)
CM
20 tháng 6 2018
Ta có: sin 40º = cos 50º ; sin 45º = cos 45º ; sin 50º = cos 40º
Do đó :
NT
2
1 tháng 7 2018
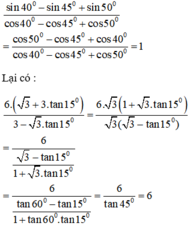
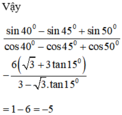
Ta có :
\(A=10^3-3^3-7^3\)
\(A=10^3-\left(3^3+7^3\right)\)
\(A=10^3-\left(3+7\right)\left(3^2-3.7+7^2\right)\)
\(A=10^3-10\left(9-21+49\right)\)
\(A=10^3-10.37\)
\(A=10\left(10^2-37\right)\)
\(A=10\left(100-37\right)\)
\(A=10.63\)
\(A=630\)
Vậy \(A=630\)
Chúc bạn học tốt ~
B
1
15 tháng 8 2023
\(log_9\left(\dfrac{1}{27}\right)=log_{3^2}3^{-3}=\dfrac{log_33^{-3}}{log_33^2}=-\dfrac{3}{2}\)
9 tháng 12 2015
\(A=\frac{\sqrt{4-2\sqrt{3}}}{\sqrt{6}-\sqrt{2}}:2\sqrt{2}=\frac{\sqrt{3-2\sqrt{3}+1}}{\sqrt{2}.\left(\sqrt{3}-1\right)}.\frac{1}{2\sqrt{2}}\)
\(=\frac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}.\left(\sqrt{3}-1\right)}.\frac{1}{2\sqrt{2}}=\frac{\sqrt{3}-1}{\sqrt{2}.\left(\sqrt{3}-1\right)}.\frac{1}{2\sqrt{2}}\)
\(=\frac{1}{2.2}=\frac{1}{4}\)
25 tháng 8 2023
a: \(6\sqrt{3}=\sqrt{108}>\sqrt{54}=3\sqrt{6}\)
\(\Rightarrow5^{6\sqrt{3}}>5^{3\sqrt{6}}\)
b: \(\sqrt{2}\cdot2^{\dfrac{2}{3}}=2^{\dfrac{1}{2}}\cdot2^{\dfrac{2}{3}}=2^{\dfrac{1}{2}+\dfrac{2}{3}}=2^{\dfrac{7}{6}}\)
\(\left(\dfrac{1}{2}\right)^{-\dfrac{4}{3}}=2^{\left(-1\right)\cdot\left(-\dfrac{4}{3}\right)}=2^{\dfrac{4}{3}}\)
mà \(\dfrac{7}{6}< \dfrac{8}{6}=\dfrac{4}{3}\).
nên \(\sqrt{2}\cdot2^{\dfrac{2}{3}}< \left(\dfrac{1}{2}\right)^{-\dfrac{4}{3}}\).
KL
0