Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(log_50,5=-0,439677\)
c) \(In\left(\dfrac{3}{2}\right)=0,405465\)

a) \(log_69+log_64=log_636=2\)
b) \(log_52-log_550=log_5\left(2:50\right)=-2\)
c) \(log_3\sqrt{5}-\dfrac{1}{2}log_550=-1,0479\)

\(a,A=log_23\cdot log_34\cdot log_45\cdot log_56\cdot log_67\cdot log_78\\ =log_28\\ =log_22^3\\ =3\\ b,B=log_22\cdot log_24...log_22^n\\ =log_22\cdot log_22^2...log_22^n\\ =1\cdot2\cdot...\cdot n\\ =n!\)

a) \(log_29\cdot log_34=4\)
b) \(log_{25}\cdot\dfrac{1}{\sqrt{5}}=-\dfrac{1}{4}\)
c) \(log_23\cdot log_9\sqrt{5}\cdot log_54=\dfrac{1}{2}\)

a) \(log_216=4\)
b) \(log_3\dfrac{1}{27}=-3\)
c) \(log1000=3\)
d) \(9^{log_312}=144\)

a) \(1,2^{1,5}=1,314534\)
b) \(10^{\sqrt{3}}=53,957374\)
c) \(\left(0,5\right)^{-\dfrac{2}{3}}=1,587401\)

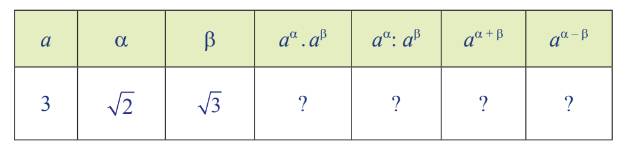
a)
| a | α | b | \(a^{\alpha}\cdot a^{\beta}\) | \(a^{\alpha}:a^{\beta}\) | \(a^{\alpha+\beta}\) | \(\alpha^{\alpha+\beta}\) |
| 3 | \(\sqrt{2}\) | \(\sqrt{3}\) | \(3^{\sqrt{2}}\cdot3^{\sqrt{3}}=31,70659\) | \(3^{\sqrt{2}}:3^{\sqrt{3}}=0,70527\) | \(3^{\sqrt{2}+\sqrt{3}}=31,70659\) | \(3^{\sqrt{2}-\sqrt{3}}=0,70527\) |
b) Nhận xét:
\(a^m\cdot a^n=a^{m+n};a^m:a^n=a^{m-n}\)

\(x=log_aN\\ \Leftrightarrow a^x=N\\ \Leftrightarrow loga^x=logN\\ \Leftrightarrow xloga=logN\\ \Leftrightarrow x=\dfrac{logN}{loga}\)
Vậy \(log_aN=\dfrac{logN}{loga}\)

\(P=loga^3+logb^2=log\left(a^3b^2\right)=log\left(100\right)=10\)
a) \(log_315=2,4650\)
c) \(3In2=2,0794\)