Cho A = 2 + 2 2 + 2 3 + . . . + 2 60 . Chứng minh A ⋮ 3, A ⋮ 7 và A ⋮ 42
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LH
0
DC
Cho A = 2 + 22 + 23 + … + 260 . Chứng minh A chia hết cho 3 ; A chia hết cho 7 và A chia hết cho 42.
2
10 tháng 11 2017
A = (2+2^2)+(2^3+2^4)+....+(2^59+2^60)
= 2.3 + 2^3.3 + .... + 2^59 .3 = 3.(2+2^2+....+2^59) chia hết cho 3
A = (2+2^2+2^3)+(2^4+2^5+2^6)+.....+(2^58+2^59+2^60)
= 2.7 + 2^4.7 + .... +2^58.7 = 7.(2+2^4+....+2^58) chia hết cho 7
Dễ thấy A chia hết cho 2 mà lại có A chia hết cho 3;7 ( cm trên )
=> A chia hết cho 2.3.7 = 42 ( vì 2;3;7 là 2 số nguyên tố cùng nhau )
MT
2
PT
1
28 tháng 4 2015
A= (21+22+23)+(24+25+26)+...+(258+259+260)
=20(21+22+23)+23(21+22+23)+...+257(21+22+23)
=(21+22+23)(20+23+...+257)
= 14(20+23+...+257) chia hết cho 7
Vậy A chia hết cho 7
25 tháng 6 2015
gọi 1/41+1/42+1/43+...+1/80=S
ta có :
S>1/60+1/60+1/60+...+1/60
S>1/60 x 40
S>8/12>7/12
Vậy S>7/12
28 tháng 12 2015
a)116+115=(..................1)+(..................1)=..........................2
Vì có chữ số tận cùng là 2 nên chia hết cho 4
NN
28 tháng 12 2015
Bài này thì chắc phải dùng đồng dư -_-
a) Ta có:
11 đồng dư với -1 (mod 4) => 115 đồng dư với (-1)5 = -1 (mod 4) => 115 + 1 chia hết cho 4
=> 116 đồng dư với (-1)6 (mod 4)
=> 116 đồng dư với 1 (mod 4)
=> 116 - 1 chia hết cho 4
=> (116 - 1) + (115 + 1) chia hết cho 4
=> 116 + 115 chia hết cho 4
12 tháng 1 2017
Bài 1 :
chứng minh A = 2 + 2^2 + 2^3 + ........... + 2^2009 + 2^2010 chia hết 42
ta thấy 42 = 2 x 3 x 7
A chia hết 42 suy ra A phải chia hết cho 2;3;7
mà ta thấy tổng trên chia hết cho 2 suy ra A chia hết cho 2 (1)
số số hạng ở tổng A là : ( 2010 - 1 ) : 1 + 1 = 2010 ( số )
ta chia tổng trên thành các nhóm mỗi nhóm 2 số ta được số nhóm là : 2010 : 2 = 1005 ( nhóm )
suy ra A = ( 2 + 2^2 ) + ( 2^3 + 2^4 ) + ...............+ ( 2^2009 + 2^2010 )
A = 2 x ( 1 + 2 ) + 2^3 x ( 1 + 2 ) + ................. + 2^2009 x ( 1 + 2 )
A = 2 x 3 + 2^3 x 3 + ............. + 2^2009 x 3
A = 3 x ( 2 + 2^3 + ........... + 2^2009 ) chia hết cho 3
suy ra A chia hết cho 3 ( 2 )
ta chia nhóm trên thành các nhóm mỗi nhóm 3 số ta có số nhóm là : 2010 : 3 = 670 ( nhóm )
suy ra A = ( 2 + 2^2 + 2^3 ) + ( 2^4 + 2^5 + 2^6 ) + ................. + ( 2^2008 + 2^2009 + 2^2010 )
A = 2 x ( 1 + 2 + 2^2 ) + 2^4 x ( 1 + 2 + 2^2 ) + .................. + 2^2008 x ( 1 + 2 + 2^2 )
A = 2 x ( 1 + 2 + 4 ) + 2^4 x ( 1 + 2 + 4 ) + ................ + 2^2008 x ( 1 + 2 + 4 )
A = 2 x 7 + 2^4 x 7 + ............. + 2^2008 x 7
A = 7 x ( 1 + 2^4 + ........ + 2^2008 ) chia hết cho 7
suy ra A chia hết cho 7 (3)
từ (1) ; (2) và (3) suy ra A chia hết cho 2;3;7
suy ra A chia hết cho 42 ( điều phải chứng minh )
BH
1
XO
14 tháng 10 2019
Ta có : A = 2 + 22 + 23 + 24 + ... + 259 + 260
= (2 + 22) + (23 + 24) + .... + (259 + 260)
= (2 + 22) + 22.(2 + 22) + ... + 258.(2 + 22)
= 6 + 22.6 + ... + 258 . 6
= 6.(1 + 22 + .... + 258)
= 2.3.(1 + 22 + .... + 258) \(⋮\)3
=> A \(⋮\)3 (đpcm)
Lại có : A = 2 + 22 + 23 + 24 + 25 + 26 + ... + 258 + 259 + 260
= (2 + 22 + 23) + (24 + 25 + 26) + ... + (258 + 259 + 260)
= (2 + 22 + 23) + 23. (2 + 22 + 23) + .... + 257. (2 + 22 + 23)
= 14 + 23.14 + .... + 257.14
= 14.(1 + 23 + ... + 257)
= 2.7.(1 + 23 + ... + 257) \(⋮\)7
=> A \(⋮\)7 (đpcm)
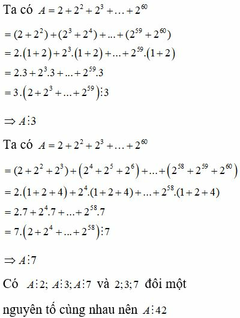
Ta có A = 2 + 2 2 + 2 3 + . . . + 2 60
= 2 + 2 2 + 2 3 + 2 4 + . . . + 2 59 + 2 60
= 2.(1+2)+ 2 3 .(1+2)+...+ 2 59 .(1+2)
= 2.3+ 2 3 .3+...+ 2 59 .3
= 3.(2+ 2 3 +...+ 2 59 ) ⋮ 3
=> A ⋮ 3
Ta có A = 2 + 2 2 + 2 3 + . . . + 2 60
= 2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + ... + 2 58 + 2 59 + 2 60
= 2.(1+2+4) + 2 4 .(1+2+4) + ... + 2 58 .(1+2+4)
= 2.7 + 2 4 .7 + ... + 2 58 .7
= 7.(2 + 2 4 + ... + 2 58 ) ⋮ 7
=> A ⋮ 7
Có A ⋮ 2; A ⋮ 3; A ⋮ 7 và 2;3;7 đôi một nguyên tố cùng nhau nên A ⋮ 42