Trong không gian với hệ trục toạ độ (Oxyz), cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9, điểm A (0; 0; 2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là hình tròn (C) có diện tích nhỏ nhất là: A. (P):x+2y+3z+6=0. B. (P):x+2y+z-2=0. C. (P):x-2y+z-6=0. ...
Đọc tiếp
Trong không gian với hệ trục toạ độ (Oxyz), cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9, điểm A (0; 0; 2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là hình tròn (C) có diện tích nhỏ nhất là:
A. (P):x+2y+3z+6=0.
B. (P):x+2y+z-2=0.
C. (P):x-2y+z-6=0.
D. (P):3x+2y+2z-4=0.
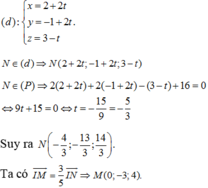
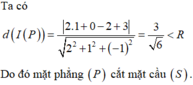
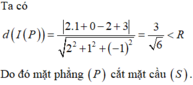
Chọn B
Mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9 có tâm I (1;2;3), bán kính R=3.
IA = √6 < R nên A nằm trong mặt cầu.
Gọi r là bán kính đường tròn thiết diện, ta có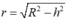
Trong đó h là khoảng cách từ I đến (P).
Diện tích thiết diện là
Vậy diện tích hình tròn (C) đạt nhỏ nhất khi h = IA. Khi đó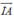
là véc tơ pháp tuyến của (P).
Phương trình mặt phẳng (P) là 1 (x-0)+2 (y-0)+ (z-2)=0 ó x + 2y + z – 2 = 0