Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi E, F lần lượt là trung điểm của AB và SC; I, J lần lượt là giao điểm của AF và EF với mặt phẳng (SBD). Tỉ số IA/IF bằng:
A. 1
B. 2
C. 3
D. 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 12 2019
Trong mặt phẳng (ABCD) : BD ∩ EC = K
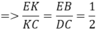
Trong mặt phẳng (SEC) : EF ∩ SK = J. Áp dụng định lí Me-nê-la-uýt vào tam giác EFC ta được: EJ/JF = 1
Đáp án B
CM
17 tháng 6 2018
Chứng minh B, J, I thẳng hàng. Áp dụng định lí Mê-nê-la-uýt vào tam giác IAB ta được IJ/JB = 1/4.
Đáp án C
CM
1 tháng 12 2018
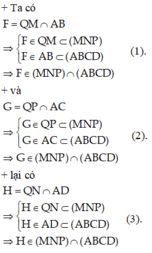
Từ (1) (2) và (3) suy ra ba điểm F, G, H thuộc giao tuyến của hai mặt phẳng (MNP) và (ABCD).
Do đó ba điểm F, G, H thẳng hàng và G nằm giữa F và H.
Chọn C.
CM
23 tháng 8 2019
Đáp án A
Dễ thấy SAEC = 1 2 SABC = 1 4 SABCD
=> SAECF = 1 2 SABCD
VS.AECF = 1 2 VS.ABC
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
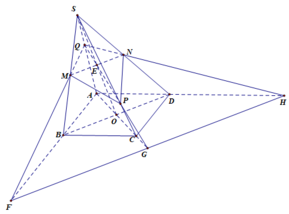
a) Gọi \(E\) là giao điểm của \(SO\) và \(MN\). Ta có:
\(\left. \begin{array}{l}E \in MN \subset \left( {MNP} \right)\\E \in S{\rm{O}}\end{array} \right\} \Rightarrow E = S{\rm{O}} \cap \left( {MNP} \right)\)
b) Gọi \(Q\) là giao điểm của \(SA\) và \(EP\). Ta có:
\(\left. \begin{array}{l}Q \in EP \subset \left( {MNP} \right)\\Q \in S{\rm{A}}\end{array} \right\} \Rightarrow Q = S{\rm{A}} \cap \left( {MNP} \right)\)
c) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in QM \subset \left( {MNP} \right)\\I \in AB \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow I \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}J \in QP \subset \left( {MNP} \right)\\J \in AC \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow J \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}K \in QN \subset \left( {MNP} \right)\\K \in AD \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow K \in \left( {MNP} \right) \cap \left( {ABCD} \right)\end{array}\)
Do đó, \(I,J,K\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {ABCD} \right)\).
Vậy \(I,J,K\) thẳng hàng.
CM
14 tháng 2 2017
Chọn C.
+) Ta có, IJ là đường trung bình tam giác SAB nên IJ // AB. ⇒ D đúng.
+) ABCD là hình bình hành nên AB// CD. Mà IJ// AB
Suy ra , IJ // CD ⇒ B đúng.
+) EF là đường trung bình tam giác SCD nên EF // CD.
Suy ra, IJ // EF ⇒ A. đúng.
- Do đó chọn đáp án C.
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1
Bài này biểu diễn ngược hơi mệt xíu, cộng trừ mấy lần mới ra:
Gọi O là tâm đáy thì \(\overrightarrow{SO}=\dfrac{1}{2}\overrightarrow{SA}+\dfrac{1}{2}\overrightarrow{SC}=\dfrac{1}{2}\overrightarrow{SB}+\dfrac{1}{2}\overrightarrow{SD}\) (1)
\(\Rightarrow\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}\) (2)
Bây giờ tìm cách đưa \(\overrightarrow{SA};\overrightarrow{SB};\overrightarrow{SC};\overrightarrow{SD}\) biểu diễn qua \(\overrightarrow{SM};\overrightarrow{SN};\overrightarrow{SG}\) là được
Với \(\overrightarrow{SB};\overrightarrow{SD}\) đơn giản: \(\overrightarrow{SB}+\overrightarrow{SD}=2\overrightarrow{SO}=3\overrightarrow{SG}\)
\(\overrightarrow{SA}=\overrightarrow{SM}+\overrightarrow{MA}=\overrightarrow{SM}+\overrightarrow{ON}=\overrightarrow{SM}+\overrightarrow{OS}+\overrightarrow{SN}=\overrightarrow{SM}-\dfrac{3}{2}\overrightarrow{SG}+\overrightarrow{SN}\)
Đặt \(\overrightarrow{SC}=x.\overrightarrow{SH}\)
Thế vào (2):
\(\Rightarrow\overrightarrow{SM}-\dfrac{3}{2}\overrightarrow{SG}+\overrightarrow{SN}+x.\overrightarrow{SH}=3\overrightarrow{SG}\)
\(\Rightarrow\overrightarrow{SM}=\dfrac{9}{2}\overrightarrow{SG}-\overrightarrow{SN}-x.\overrightarrow{SH}\)
Trong mặt phẳng (SAC) : AF ∩S O = I là trọng tâm tam giác SBD ⇒ IA/IF=2
Đáp án B