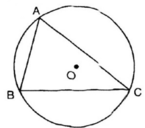
Cho tam giác nhọn ABC nội tiếp đường tròn(O). Các cung nhỏ AB, BC, CA có số đo lần lượt là x + 75 0 , 2 x + 25 0 , 3 x - 22 ° . Một góc của tam giác ABC có số đo là:
( A ) 57 ° 5 ( B ) 59 ° ; ( C ) 61 ° ; ( D ) 60 °
Hãy chọn câu trả lời đúng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các cung 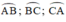 tạo thành một đường tròn
tạo thành một đường tròn
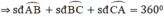
⇒ x + 75 ° + 2 x + 25 ° + 3 x − 22 ° = 360 ° ⇒ 6 x = 282 ° ⇒ x = 47 °
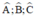 là các góc nội tiếp chắn các cung
là các góc nội tiếp chắn các cung 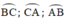
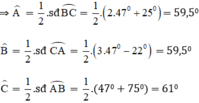
Vậy chọn đáp án C.

Lời giải:
Ta có:
$x+10^0+x+20^0+x+30^0=360^0$
$\Rightarrow 3x+60^0=360^0$
$\RIghtarrow x=100^0$
$\widehat{ABC}=\frac{1}{2}\text{sđc(AC)}=\frac{1}{2}(x+30^0)=\frac{1}{2}(100^0+30^0)=65^0$
$\widehat{ACB}=\frac{1}{2}\text{sđc(AB)}=\frac{1}{2}(x+10^0)=\frac{1}{2}(100^0+10^0)=55^0$
$\widehat{BAC}=180^0-\widehat{ABC}-\widehat{ACB}=180^0-65^0-55^0=60^0$

Hướng dẫn làm bài:
Vì các cung AB, BC, CA tạo thành đường tròn, do đó:
(x + 75°) + (2x + 25°) + (3x - 22°) = 360°
⇔ 6x + 78° = 360° ⇔ 6x = 282° ⇔ x = 47°
Vậy sđ cung AB = x + 75° = 47° + 75° = 122°
⇒ˆC=12202=610⇒C^=12202=610
sđ cung BC = 2x + 25° = 2.47° + 25° = 119° ⇒ˆA=11902=59,50⇒A^=11902=59,50
sđ cung AC = 3x - 22° = 3.47° - 22° = 119° ⇒ˆB=11902=59,50⇒B^=11902=59,50
Chọn đáp án C

1: AB=AC
NB=NC
=>AN là trung trực của BC
mà O nằm trên trung trực của BC
nên A,N,O thẳng hàng
=>AN là đường kính của (O)
=>góc ABN=90 độ
2: góc BIN=1/2(sđ cung BN+sđ cung AP)
=1/2(sđ cungCN+sđ cung CP)
=1/2*sđ cung PN
=góc IBN
=>ΔIBN cân tại N

a) Ta có: AE,AF là tiếp tuyến \(\Rightarrow AE=AF\Rightarrow\Delta AEF\) cân tại A
\(\Rightarrow\angle AEF=\angle AFE\Rightarrow\angle BFX=\angle CEY\)
Xét \(\Delta BFX\) và \(\Delta CEY:\) Ta có: \(\left\{{}\begin{matrix}\angle BFX=\angle CEY\\\angle BXF=\angle CYE=90\end{matrix}\right.\)
\(\Rightarrow\Delta BFX\sim\Delta CEY\left(g-g\right)\Rightarrow\dfrac{BF}{CE}=\dfrac{BX}{CY}\)
mà \(\left\{{}\begin{matrix}BF=BD\\CE=CD\end{matrix}\right.\) (tính chất tiếp tuyến) \(\Rightarrow\dfrac{BD}{CD}=\dfrac{BX}{CY}\)
Vì \(BX\parallel DK\parallel CY\) \(\Rightarrow\dfrac{XK}{KY}=\dfrac{BD}{CD}\Rightarrow\dfrac{BX}{CY}=\dfrac{XK}{KY}\)
Xét \(\Delta BKX\) và \(\Delta CKY:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{BK}{CY}=\dfrac{KX}{KY}\\\angle BXK=\angle CYK=90\end{matrix}\right.\)
\(\Rightarrow\Delta BKX\sim\Delta CKY\left(c-g-c\right)\Rightarrow\angle BKX=\angle CKY\)
\(\Rightarrow90-\angle BKX=90-\angle CKY\Rightarrow\angle BKD=\angle CKD\)
\(\Rightarrow\dfrac{BK}{KC}=\dfrac{BD}{CD}\Rightarrow BD.CK=BK.CD\)


Bạn mở trong đường link này sẽ có https://moon.vn/hoi-dap/cho-tam-giac-deu-abc-noi-tiep-trong-duong-tron-tam-o-goi-mnp-lan-luot-la-trung-diem--665623
( Hình hơi bị lệch một xíu, tam giác không chính xác lắm nha)
a) Do tam giác ABC đều và M, N lần lượt là trung điểm của \(AB,BC\Rightarrow\hept{\begin{cases}OM\perp AB\\ON\perp BC\end{cases}\Rightarrow\widehat{OMB}=\widehat{ONB}=90^o}\)
Xét tứ giác BMON có: \(\widehat{OMB}+\widehat{ONB}=180^o\) suy ra tứ giác BMON là tứ giác nội tiếp (tứ giác cỏ tổng 2 góc đối bằng 180o
b) Do O là trọng tâm tam giác ABC(giả thiết) suy ra \(ON=\frac{OA}{2}=\frac{R}{2}\)( tính chất đường trung tuyến).
Mặt khác, \(OG=ON+NG\Rightarrow NG=OG-ON=R-\frac{R}{2}=\frac{R}{2}\)
Vậy \(NO=NG=\frac{R}{2}\left(đpcm\right)\)
c) Gọi \(E=EC\Omega PN\) ta có: \(OC\perp AB\) (do tam giác ABC đều); \(NO//AB\)( NP là đường trung bình của tam giác ABC)
\(\Rightarrow OC\perp NP\) tại E => tam giác OEF vuông tại E.
Xét tam giác ONC vuông tại N có đường cao NE ta có: \(ON^2=OE.OC\Rightarrow OE=\frac{ON^2}{OC}=\frac{R}{4}\) (hệ thức lượng)
Xét tam giác vuông OEF có: \(\sin\widehat{OFE}=\sin\widehat{OFP}=\frac{OE}{OF}=\frac{R}{\frac{4}{R}}=\frac{1}{4}\Rightarrow\widehat{OFP}\approx14^O28'\)

Tứ giác ABMC nội tiếp \(\Rightarrow\widehat{ABM}+\widehat{ACM}=180^0\)
Mà \(\widehat{ACM}+\widehat{MCE}=180^0\Rightarrow\widehat{ABM}=\widehat{MCE}\)
D và E cùng nhìn CM dưới 1 góc vuông \(\Rightarrow CDME\) nội tiếp
\(\Rightarrow\widehat{MCE}=\widehat{MDE}\) (cùng chắn ME) \(\Rightarrow\widehat{ABM}=\widehat{MDE}\)
Mặt khác D và F cùng nhìn BM dưới 1 góc vuông \(\Rightarrow BFDM\) nội tiếp
\(\Rightarrow\widehat{ABM}+\widehat{FDM}=180^0\)
\(\Rightarrow\widehat{MDE}+\widehat{FDM}=180^0\Rightarrow\) D, E, F thẳng hàng
Các cung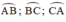 tạo thành một đường tròn
tạo thành một đường tròn
⇒ x + 75 ° + 2 x + 25 ° + 3 x − 22 ° = 360 ° ⇒ 6 x = 282 ° ⇒ x = 47 °
Vậy chọn đáp án C.