Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
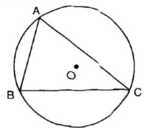
Các cung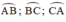 
tạo thành một đường tròn
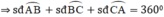
⇒ x + 75 ° + 2 x + 25 ° + 3 x − 22 ° = 360 ° ⇒ 6 x = 282 ° ⇒ x = 47 °
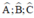là các góc nội tiếp chắn các cung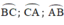 
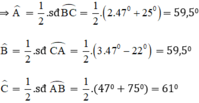
Vậy chọn đáp án C.
Hướng dẫn làm bài:
Vì các cung AB, BC, CA tạo thành đường tròn, do đó:
(x + 75°) + (2x + 25°) + (3x - 22°) = 360°
⇔ 6x + 78° = 360° ⇔ 6x = 282° ⇔ x = 47°
Vậy sđ cung AB = x + 75° = 47° + 75° = 122°
⇒ˆC=12202=610⇒C^=12202=610
sđ cung BC = 2x + 25° = 2.47° + 25° = 119° ⇒ˆA=11902=59,50⇒A^=11902=59,50
sđ cung AC = 3x - 22° = 3.47° - 22° = 119° ⇒ˆB=11902=59,50⇒B^=11902=59,50
Chọn đáp án C
Lời giải:
Ta có:
$x+10^0+x+20^0+x+30^0=360^0$
$\Rightarrow 3x+60^0=360^0$
$\RIghtarrow x=100^0$
$\widehat{ABC}=\frac{1}{2}\text{sđc(AC)}=\frac{1}{2}(x+30^0)=\frac{1}{2}(100^0+30^0)=65^0$
$\widehat{ACB}=\frac{1}{2}\text{sđc(AB)}=\frac{1}{2}(x+10^0)=\frac{1}{2}(100^0+10^0)=55^0$
$\widehat{BAC}=180^0-\widehat{ABC}-\widehat{ACB}=180^0-65^0-55^0=60^0$
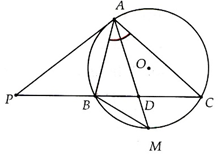
a: sđ cung nhỏ AB=2*30=60 độ
sđ cung lớn AB là 360-60=300 độ
góc PAB=góc BCA=30 độ
góc AOB=sđ cung nhỏ AB=60 độ
b,c: Bạn ghi lại đề đi bạn
a) Xét (O) có
\(\widehat{DBE}\) là góc nội tiếp chắn \(\stackrel\frown{DE}\)
Do đó: \(\widehat{DBE}=\dfrac{1}{2}\cdot sđ\stackrel\frown{DE}\)(Định lí góc nội tiếp)
\(\Leftrightarrow\widehat{DBE}=\dfrac{1}{2}\cdot60^0=30^0\)
Xét (O) có
ΔBEC nội tiếp đường tròn(B,E,C∈(O))
BC là đường kính(gt)
Do đó: ΔBEC vuông tại E(Định lí)
⇒BE⊥CE tại E
hay BE⊥AC tại E
Ta có: ΔAEB vuông tại E(BE⊥AC tại E)
nên \(\widehat{EAB}+\widehat{ABE}=90^0\)(hai góc nhọn phụ nhau)
⇒\(\widehat{BAC}=90^0-\widehat{ABE}=90^0-30^0\)
⇒\(\widehat{BAC}=60^0\)
Vậy: \(\widehat{BAC}=60^0\)
Các cung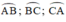
tạo thành một đường tròn
⇒ x + 75 ° + 2 x + 25 ° + 3 x − 22 ° = 360 ° ⇒ 6 x = 282 ° ⇒ x = 47 °
Vậy chọn đáp án C.