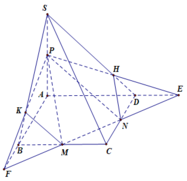
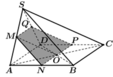
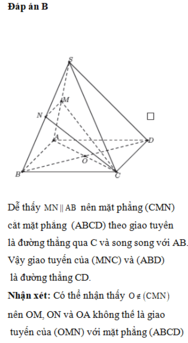
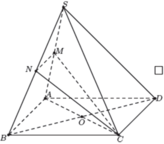
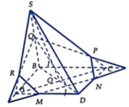
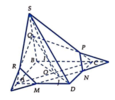
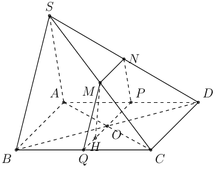
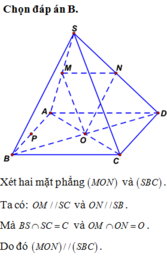
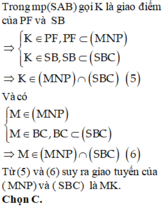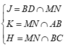Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M; N’; P lần lượt là trung điểm của các cạnh BC; CD và SA. Gọi E là giao điểm của MN và AD; F là giao điểm của MN và AB. Tìm giao tuyến của (MNP) và (SBC)
A. ME
B. MH trong đó H là giao điểm của SD và PE
C. MK trong đó K là giao điểm của SB và PF
D. đáp án khác