Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
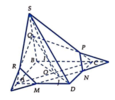
Trong (ABCD) gọi
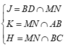
Trong (SBC) gọi: ![]()
Trong (SBD) gọi: Q = IJ ∩ SB
Trong (SBC) gọi: R = KQ ∩ SA
Suy ra, thiết diện là ngũ giác MNPQR.

MN là đường trung bình tam giác ABD \(\Rightarrow MN||BD\)
Trong mp (SBD), qua P kẻ đường thẳng song song BD lần lượt cắt SB và SD tại E và F
Gọi I là giao điểm AC mà MN
Trong mp (SAC), nối IP kéo dài cắt SC tại Q
Ngũ giác MNFQE là thiết diện của (MNP) và chóp

IJ là đường trung bình của hình thang \(\Rightarrow\left\{{}\begin{matrix}IJ||AB\\IJ=\dfrac{AB+CD}{2}\end{matrix}\right.\)
Qua G kẻ đường thẳng song song AB lần lượt cắt SB, SA tại E và F
\(\Rightarrow\) Tứ giác IJEF là thiết diện của (GIJ) và chóp
\(EF||AB||IJ\Rightarrow IJEF\) là hình thang
Gọi M là trung điểm AB
Theo tính chất trọng tâm và định lý Talet:
\(\dfrac{EF}{AB}=\dfrac{SG}{SM}=\dfrac{2}{3}\)
Để IJEF là hình bình hành \(\Leftrightarrow IJ=EF\)
\(\Leftrightarrow\dfrac{2}{3}AB=\dfrac{AB+CD}{2}\Leftrightarrow\dfrac{1}{3}AB=CD\)
\(\Rightarrow AB=3CD\)

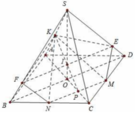
Do MN//BD nên giao tuyến của (MNK) với (SBD) song song với MN. Qua I dựng đường thẳng song song với MN cắt SD,SB lần lượt tại E và F khi đó thiết diện là ngũ giác KEMNF

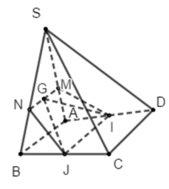
Theo câu 27, ta có MN // AB // IJ và thiết diện của mặt phẳng (GIJ) với hình chóp là tứ giác MNJI.
Ta có MN đi qua trọng tâm G cảu tam giác SAB và song song với AB nên M N A B = 2 3 = > M N = 2 3 A B
IJ là đường trung bình của hình thangABCD nên: IJ = 1 2 ( A B + C D )
Do IJ // MN nên thiết diện là hình bình hành khi và chỉ khi IJ = MN
= > 2 3 A B = 1 2 ( A B + C D )
⇒AB = 3CD
Đáp án B