Cho tam giác nhọn ABC nội tiếp đường tròn (O) với AB<AC. Đường phân giác của góc B A C ^ cắt (O) tại điểm D khác A
Gọi M là trung điểm của AD và E là điểm đối xứng với D qua tâm O.
Giả sử đường tròn ngoại tiếp tam giác ABM cắt đoạn thẳng AC tại điểm F khácA
1) Chứng minh rằng tam giác ĐM và tam giác BCF đồng dạng.

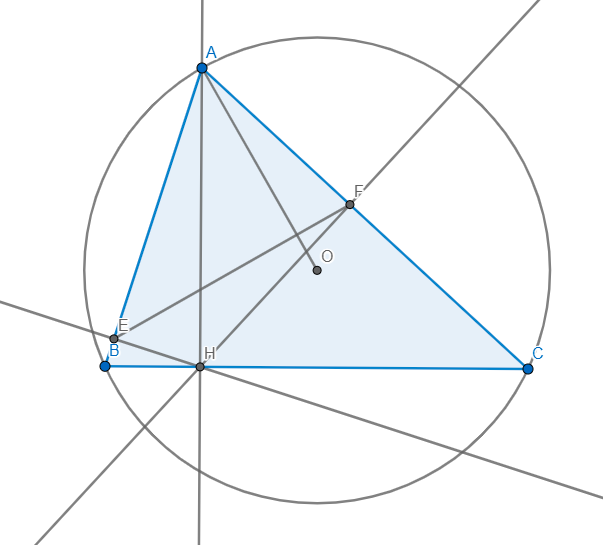
1). Ta có góc nội tiếp bằng nhau B D M ^ = B C F ^ ( 1 ) và B M A ^ = B F A ^ suy ra 180 0 − B M A ^ = 180 0 − B F A ^ hay B M D ^ = B F C ^ (2).
Từ (1) và (2), suy ra Δ B D M ~ Δ B C F (g - g).