Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\angle AEB=\angle ADB=90\Rightarrow ABDE\) nội tiếp
b) Vì AK là đường kính \(\Rightarrow\angle ACK=\angle ABK=90\)
\(\Rightarrow\left\{{}\begin{matrix}CK\bot AC\\BK\bot AB\end{matrix}\right.\) mà \(\left\{{}\begin{matrix}BH\bot AC\\CH\bot AC\end{matrix}\right.\Rightarrow\) \(BH\parallel CK,CH\parallel BK\)
\(\Rightarrow BHCK\) là hình bình hành
c) Vì F là giao điểm của CH và AB \(\Rightarrow CF\bot AB\)
Ta có: \(\dfrac{AD}{HD}+\dfrac{BE}{HE}+\dfrac{CF}{HF}=\dfrac{AD.BC}{HD.BC}+\dfrac{BE.AC}{HE.AC}+\dfrac{CF.AB}{HF.AB}\)
\(=\dfrac{S_{ABC}}{S_{HBC}}+\dfrac{S_{ABC}}{S_{AHC}}+\dfrac{S_{ABC}}{S_{AHB}}=S_{ABC}\left(\dfrac{1}{S_{HBC}}+\dfrac{1}{S_{AHC}}+\dfrac{1}{S_{AHB}}\right)\)
\(\ge S_{ABC}.\dfrac{9}{S_{HBC}+S_{HAC}+S_{AHB}}\)(BĐT Schwarz) \(=S_{ABC}.\dfrac{9}{S_{ABC}}=9\)
\(\Rightarrow Q_{min}=9\)

a: góc AEB=góc ADB=90 độ
=>ABDE nội tiếp
b: góc CBK=1/2*180=90 độ
Xet ΔCBK vuông tại B và ΔCFA vuông tại F có
góc BCK=góc FCA
=>ΔCBK đồng dạng vơi ΔCFA
=>CB/CF=CK/CA
=>CB*CA=CF*CK

a: Xét tứ giác AEHF có
góc AEH+góc AFH=180 độ
=>AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔABK nội tiếp
AK là đường kính
=>ΔABK vuông tại B
=>BK//CH
Xét (O) có
ΔACK nội tiếp
AK là đường kính
=>ΔACK vuông tại C
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
=>I là trung điểm của BC

a: Xét tứ giác ABDE có
\(\widehat{ADB}=\widehat{AEB}=90^0\)
Do đó: ABDE là tứ giác nội tiếp
b: Xét ΔDAC vuông tại D và ΔDBF vuông tại D có
\(\widehat{DAC}=\widehat{DBF}\)
Do đó:ΔDAC∼ΔDBF
Suy ra: DA/DB=DC/DF
hay \(DB\cdot DC=DA\cdot DF\)

Xét (O) có
ΔACK nội tiếp đường tròn
AK là đường kính
Do đó: ΔACK vuông tại C
Xét (O) có
ΔABK nội tiếp đường tròn
AK là đường kính
Do đó: ΔABK vuông tại B
Xét tứ giác BHCK có
BH//CK
CH//BK
Do đó: BHCK là hình bình hành

a) Xét tứ giác AEHF có
\(\widehat{HFA}\) và \(\widehat{HEA}\) là hai góc đối
\(\widehat{HFA}+\widehat{HEA}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
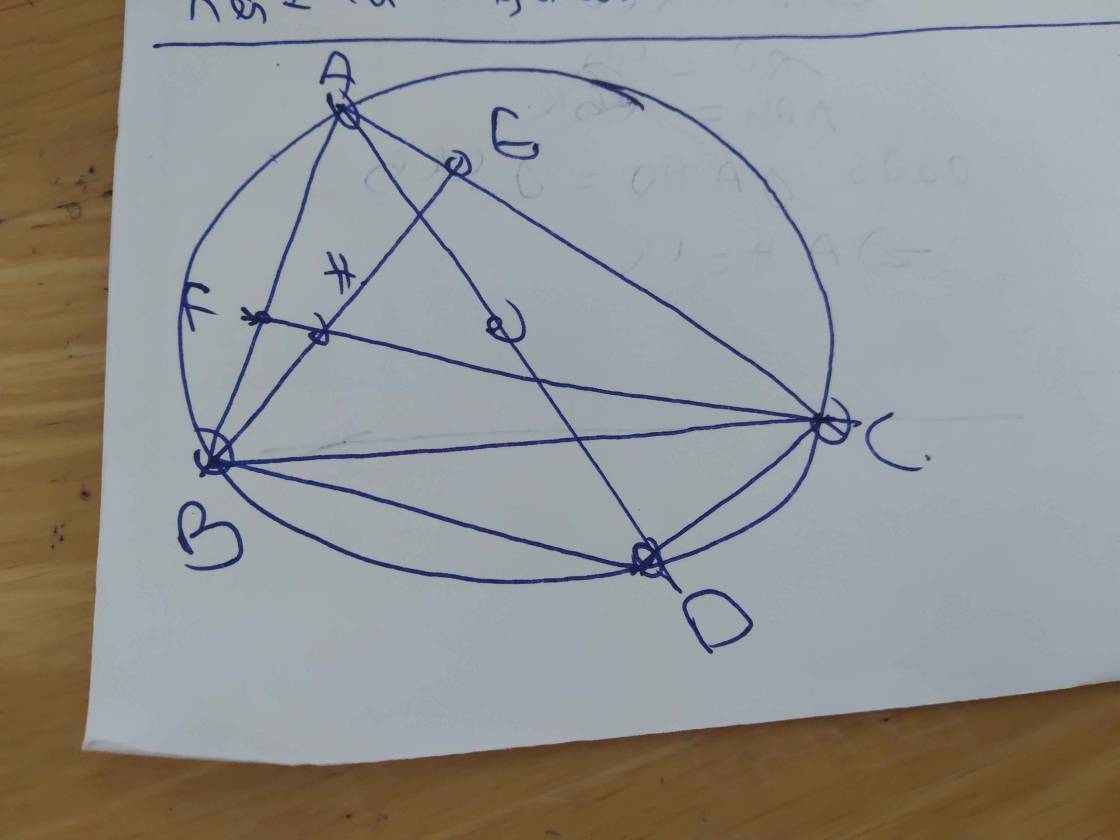


giúp mình câu b với các bạn ơi