Cho tam giác ABC nhọn Các đường cao AD,BE,CF gọi H là trực tâm của tam giác ABC (AB<AC)Chứng mỉnh rằng :\(\frac{AH}{HD}+\frac{BH}{HE}+\frac{CH}{CF}>6\)Hộ mình bài trên nhaÀ nếu có thể thì các bạn vô link này subcribe kênh mình nhé ; cảm ơn các pạn...
Đọc tiếp
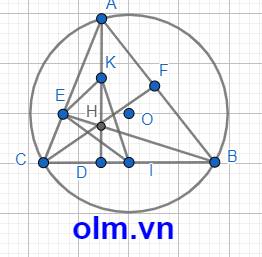
Cho tam giác ABC nhọn Các đường cao AD,BE,CF gọi H là trực tâm của tam giác ABC (AB<AC)
Chứng mỉnh rằng :
\(\frac{AH}{HD}+\frac{BH}{HE}+\frac{CH}{CF}>6\)
Hộ mình bài trên nha
À nếu có thể thì các bạn vô link này subcribe kênh mình nhé ; cảm ơn các pạn :
https://www.youtube.com/watch?v=p3ooUO9vQq8
Bài làm:
Ta có: \(\frac{AH}{HD}+\frac{BH}{HE}+\frac{CH}{HF}\)
\(=\left(\frac{AH}{HD}+1\right)+\left(\frac{BH}{HE}+1\right)+\left(\frac{CH}{HF}+1\right)-3\)
\(=\frac{AH+HD}{HD}+\frac{BH+HE}{HE}+\frac{CH+HF}{HF}-3\)
\(=\frac{AD}{HD}+\frac{BE}{HE}+\frac{CF}{HF}-3\)
\(=\frac{S_{ABC}}{S_{BHC}}+\frac{S_{ABC}}{S_{AHC}}+\frac{S_{ABC}}{S_{AHB}}-3\)
\(=S_{ABC}\left(\frac{1}{S_{BHC}}+\frac{1}{S_{AHC}}+\frac{1}{S_{AHB}}\right)-3\)
\(\ge S_{ABC}\cdot\frac{9}{S_{BHC}+S_{AHC}+S_{AHB}}-3\)
\(=S_{ABC}\cdot\frac{9}{S_{ABC}}-3\)
\(=9-3=6\)
Dấu "=" xảy ra khi H là trọng tâm tam giác ABC
=> Tam giác ABC đều => AB = AC vô lý
=> Không xảy ra dấu bằng
=> đpcm
làm giùm thì được chứ subrice là ko