cho phương trình mx2-2(m+1)x-3m+1=0
trong trường hợp m khác 0 với x1,x2 là 2 nghiệm của phương trình
tìm m để A=x12+x22 đạt giá trị nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 3 2022
\(\Delta'=\left(m+1\right)^2-2m-10=m^2-9\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-3\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=2m+10\end{matrix}\right.\)
a.
\(P=x_1^2+x_2^2+6x_1x_2=\left(x_1+x_2\right)^2+4x_1x_2\)
\(P=4\left(m+1\right)^2+4\left(2m+10\right)\)
\(P=4m^2+16m+44=\left(4m^2+16m+12\right)+32\)
\(P=4\left(m+1\right)\left(m+3\right)+32\ge32\)
\(P_{min}=32\) khi \(m=-3\)
b.
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=2m+10\end{matrix}\right.\)
Trừ vế cho vế:
\(x_1+x_2-x_1x_2=-8\)
Đây là hệ thức liên hệ 2 nghiệm ko phụ thuộc m
GH
5 tháng 7 2023
\(\Delta=\left(m+1\right)^2-4.1.2=\left(m+1\right)^2-8\)
Để PT có 2 nghiệm thì:
\(\Delta\ge0\Leftrightarrow\left(m+1\right)^2-8\ge0\\ \Leftrightarrow\left(m+1\right)^2\ge8\)
Theo vi ét: \(\left\{{}\begin{matrix}x_1+x_2=-\left(m+1\right)\\x_1x_2=2\end{matrix}\right.\)
\(x_1^2+x_2^2=x_1^2+2x_1x_2+x_2^2-2x_1x_2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(m+1\right)^2-2.2=\left(m+1\right)^2-4\)
Mà \(\left(m+1\right)^2\ge8\) nên \(\left(m+1\right)^2-4\ge4\)
\(\Rightarrow min_{x_1^2+x_2^2}=4\) (dấu bằng xảy ra)
\(\Leftrightarrow\left(m+1\right)^2=8\)
\(\Leftrightarrow m^2+2m+1=8\\\Leftrightarrow m^2+2m-7=0 \)
\(\Leftrightarrow m=-1\pm2\sqrt{2}\)
CM
22 tháng 7 2017
Phương trình có hai nghiệm
B = 2 ( x 1 2 + x 2 2 ) + 16 − 3 x 1 x 2
= 2 ( x 1 + x 2 ) 2 − 4 x 1 x 2 + 16 − 3 x 1 x 2 = 2 ( 2 m + 2 ) 2 − 4 ( m 2 + 2 ) + 16 − 3 ( m 2 + 2 ) = 4 m 2 + 16 m + 16 − 3 ( m 2 + 2 ) = 2 m + 4 − 3 ( m 2 + 2 ) = − 3 m 2 + 2 m − 2
Xét hàm số y = − 3 m 2 + 2 m − 2 với m ≥ 1 2
Bảng biến thiên
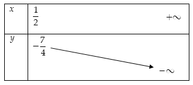
Suy ra giá trị m a x m ≥ 1 2 y = − 7 4 khi m = 1 2
Vậy giá trị lớn nhất của biểu thức B là - 7 4 khi m = 1 2
Đáp án cần chọn là: B
21 tháng 1 2023
a: Δ=(2m-1)^2-4*(-m)
=4m^2-4m+1+4m=4m^2+1>0
=>Phương trình luôn có nghiệm
b: \(A=\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2\)
\(=\left(2m-1\right)^2-3\left(-m\right)\)
=4m^2-4m+1+3m
=4m^2-m+1
=4(m^2-1/4m+1/4)
=4(m^2-2*m*1/8+1/64+15/64)
=4(m-1/8)^2+15/16>=15/16
Dấu = xảy ra khi m=1/8
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 1 2021
\(\Delta=\left(m+1\right)^2-4\left(m^2-2m+2\right)=-3m^2+10m-7\ge0\)
\(\Rightarrow1\le m\le\dfrac{7}{3}\)
\(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1x_2=m^2-2m+2\end{matrix}\right.\)
\(P=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(m+1\right)^2-2\left(m^2-2m+2\right)\)
\(=-m^2+6m-3\)
\(=\left(-m^2+6m-\dfrac{77}{9}\right)+\dfrac{50}{9}\)
\(=\left(\dfrac{11}{3}-m\right)\left(m-\dfrac{7}{3}\right)+\dfrac{50}{9}\le\dfrac{50}{9}\)
\(P_{max}=\dfrac{50}{9}\) khi \(m=\dfrac{7}{3}\)
1 tháng 3 2022
-mình sửa đề luôn nhé
\(\Delta=9m^2-4\left(3m-2\right)=9m^2-12m+8=\left(3m-2\right)^2+4>0\)
Vậy pt luôn có 2 nghiệm pb
Vì x1 là nghiệm pt trên nên
\(A=3mx_1-3m+2+3mx_2-m+1=3m.3m-4m+3\)
\(=9m^2-4m+3=9m^2-\dfrac{2.3m.4}{6}+\dfrac{16}{36}-\dfrac{16}{36}+3\)
\(=\left(3m-\dfrac{4}{6}\right)^2+\dfrac{23}{9}\ge\dfrac{23}{9}\)Dấu ''='' xảy ra khi m = 2/9
GH
5 tháng 7 2023
Bổ sung thêm điều kiện đề với \(m\ne1\) nữa nhé: )
Nhẩm nghiệm: \(a-b+c=0\) \(\left(m-1-m-1+2=0\right)\)
\(\Rightarrow\) PT có 2 nghiệm \(x_1=-1;x_2=\dfrac{2}{m-1}\)
Nếu \(x_1^2-x_2^2=3\):
\(\left(-1\right)^2-\left(\dfrac{2}{m-1}\right)^2=3\)
=> Không có giá trị m thỏa mãn.
Nếu \(x_1^2-x_2^2=-3\):
\(\left(-1\right)^2-\left(\dfrac{2}{m-1}\right)^2=-3\\ \Rightarrow m=2\left(TM\right)\)