Question

[nguyễn hoàng lê thi]

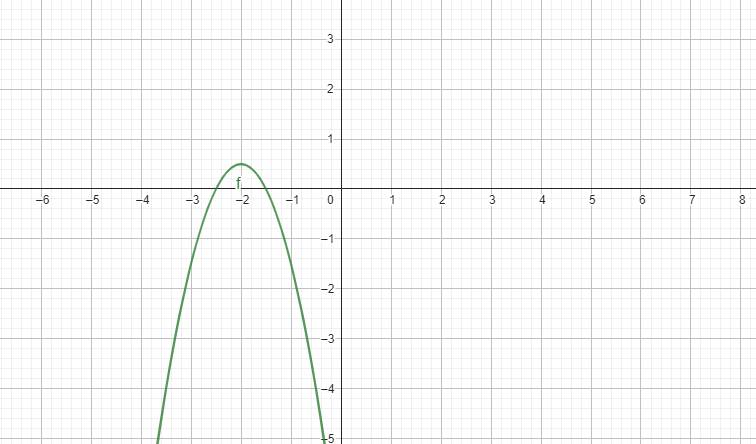
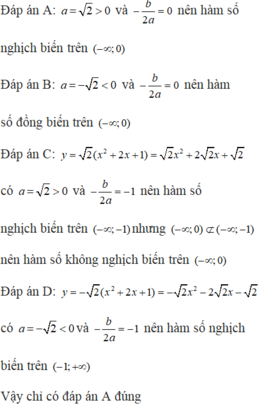1. Hàm số nào sau đây nghịch biến trong khoảng ( âm vô cùng ; 0)

A. y = √2 x² +1

B. y = - √2 . x² +1

C. y = √2 ( x +1)²

D. y = -√2 ( x+1)²

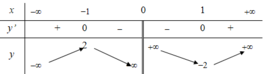
2. Cho hàm số y = x² - 2x +3. Trong các mệnh đề sau , tìm mệnh đề đúng

A. y tăng trên trên ( 0; âm vô cùng)

B. y giảm trên ( âm vô cỳng ; 2)

C. Đồ Đồ thị của y có đỉnh I ( 1;0)

D. y tăng trên ( 2; dương vô cùng)

3. Parabol y = ax^2 + bx + 2 đi qua hai điểm M(1;5) và N(-2;8) có phương trình là?

A. y = x^^2 + x +2

B. y = x^2 +2x +2

C. y= 2x^2 + x +2

D. y= 2x^2 +2x +2