Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

làm luôn nha :
a) đặc : \(f\left(x\right)=y=-x^2-4x-5\)
ta chọn \(a=-3;b=-4\) thuộc \(\left(-\infty;-2\right)\)
\(\Rightarrow\dfrac{f\left(a\right)-f\left(b\right)}{a-b}=\dfrac{-\left(-3\right)^2-4\left(-3\right)-5-\left(-\left(-4\right)^2-4\left(-4\right)-5\right)}{-3-\left(-4\right)}=3\)
\(\Rightarrow\) hàm số này đồng biến .
b) đặc \(f\left(x\right)=y=\dfrac{x+2}{x-1}\)
ta chọn \(a=-1;b=0\) thuộc \(\left(-\infty;1\right)\)
\(\Rightarrow\dfrac{f\left(a\right)-f\left(b\right)}{a-b}=\dfrac{\dfrac{-1+2}{-1-1}-\dfrac{0+2}{0-1}}{-1}=\dfrac{-3}{2}\)\(\Rightarrow\) hàm số này nghịch biến .
làm cách không chọn giá trị theo yc :
a) đặc : \(f\left(x\right)=y=-x^2-4x-5\)
giả sử : \(a< b< -2\)
khi đó ta có : \(\dfrac{f\left(a\right)-f\left(b\right)}{a-b}=\dfrac{-a^2-4a-5-\left(-b^2-4b-5\right)}{a-b}\)
\(\dfrac{b^2-a^2+4b-4a}{a-b}=\dfrac{\left(b-a\right)\left(a+b\right)+4\left(b-a\right)}{a-b}\)
\(=\dfrac{-\left(a+b+4\right)\left(a-b\right)}{a-b}=-\left(a+b+4\right)\)
vì \(a< b< -2\Rightarrow a+b< -4\Rightarrow a+b+4< 0\Rightarrow-\left(a+b+4\right)>0\)
\(\Rightarrow\) hàm số đồng biến
b) đặc : \(f\left(x\right)=y=\dfrac{x+2}{x-1}\)
giả sử : \(a< b< 1\)
khi đó ta có : \(\dfrac{f\left(a\right)-f\left(b\right)}{a-b}=\dfrac{\dfrac{a+2}{a-1}-\dfrac{b+2}{b-1}}{a-b}\)
\(\dfrac{\dfrac{3b-3a}{\left(a-1\right)\left(b-1\right)}}{a-b}=\dfrac{3\left(b-a\right)}{\left(a-1\right)\left(b-1\right)\left(a-b\right)}\)
\(=\dfrac{-3}{\left(a-1\right)\left(b-1\right)}\)
vì \(a< b< 1\Rightarrow\left(a-1\right);\left(b-1\right)< 0\) \(\Rightarrow\left(a-1\right)\left(b-1\right)>0\)
\(\Rightarrow\dfrac{-3}{\left(a-1\right)\left(b-1\right)}< 0\)
\(\Rightarrow\) hàm số nghịch biến

a) \(y = - {x^2} + 6x - 9\)
Ta có: \(a = - 1\) nên parabol quay bề lõm xuống dưới.
Đỉnh \(I\left( {3;0} \right).\) Trục đối xứng \(x = 3.\) Giao điểm của đồ thị với trục \(Oy\) là: \(A\left( {0; - 9} \right).\) Parabol cắt trục hoành tại \(x = 3.\)
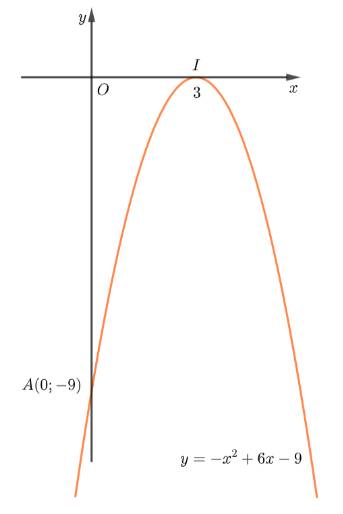
Tập giá trị của hàm số là: \(\left( { - \infty ;0} \right].\)
Từ đồ thị ta thấy: Hàm số \(y = - {x^2} + 6x - 9\) đồng biến trên khoảng \(\left( { - \infty ;3} \right)\) và nghịch biến trên khoảng \(\left( {3; + \infty } \right).\)
b) \(y = - {x^2} - 4x + 1\)
Ta có: \(a = - 1\) nên parabol quay bề lõm xuống dưới.
Đỉnh \(I\left( { - 2;5} \right).\) Trục đối xứng \(x = - 2.\) Giao điểm của hàm số với trục \(Oy\) là: \(\left( {0;1} \right).\) Giao điểm của hàm số với trục \(Ox\) là: \(x = - 2 + \sqrt 5 \) và \(x = - 2 - \sqrt 5 .\)
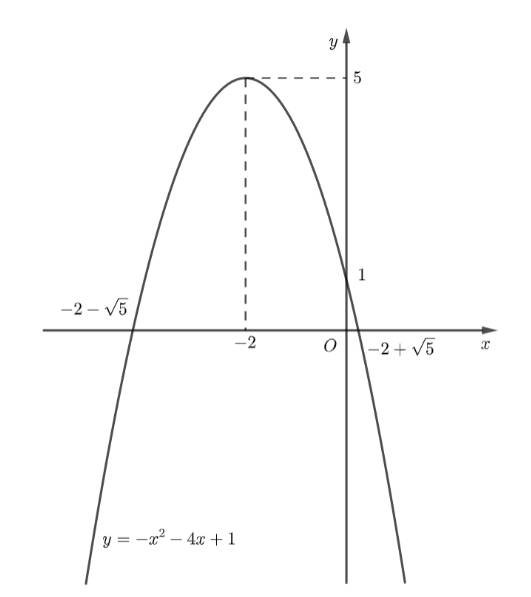
Tập giá trị của hàm số là: \(\left( { - \infty ;5} \right].\)
Từ đồ thị ta thấy: Hàm số \(y = - {x^2} - 4x + 1\) đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\) và nghịch biến trên khoảng \(\left( { - 2; + \infty } \right).\)
c) \(y = {x^2} + 4x\)
Ta có: \(a = 1 > 0\) nên parabol quay bề lõm lên trên.
Đỉnh \(I\left( { - 2; - 4} \right).\) Trục đối xứng \(x = - 2.\) Giao điểm của hàm số với trục \(Oy\) là: \(\left( {0;0} \right).\) Giao điểm của hàm số với trục \(Ox\) là: \(x = 0\) và \(x = - 4.\)
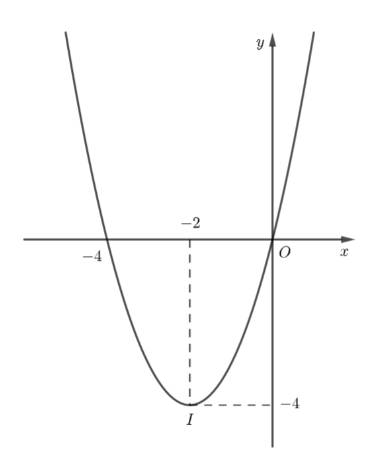
Tập giá trị của hàm số là: \(\left[ { - 4; + \infty } \right).\)
Từ đồ thị ta thấy: Hàm số \(y = {x^2} + 4x\) đồng biến trên khoảng \(\left( { - 2; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right).\)
d) \(y = 2{x^2} + 2x + 1\)
Ta có: \(a = 2 > 0\) nên parabol quay bề lõm lên trên.
Đỉnh \(I\left( { - \frac{1}{2};\frac{1}{2}} \right).\) Trục đối xứng \(x = - \frac{1}{2}.\) giao điểm của hàm số với trục \(Oy\) là: \(\left( {0;1} \right).\) Đồ thị hàm số không có giao điểm với trục \(Ox.\) Lấy điểm \(\left( {1;5} \right)\) thuộc đồ thị hàm số, điểm đối xứng với điểm đó qua trục đối xứng \(x = - \frac{1}{2}\) là: \(\left( { - 2;5} \right).\)
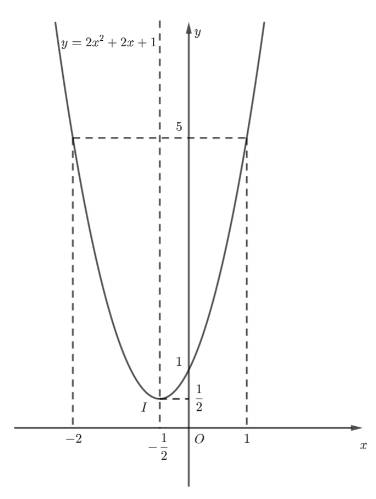
Tập giá trị của hàm số là: \(\left[ {\frac{1}{2}; + \infty } \right).\)
Từ đồ thị ta thấy: Hàm số \(y = 2{x^2} + 2x + 1\) đồng biến trên khoảng \(\left( { - \frac{1}{2}; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ; - \frac{1}{2}} \right).\)


1. \(y=f\left(x\right)=x^2+2\left|x\right|-1\)
TXĐ: D=R
a) Xét tính chẵn lẻ
Với mọi x thuộc D => -x thuộc D
Xét : \(f\left(-x\right)=\left(-x\right)^2+2\left|-x\right|-1=x^2+2\left|x\right|-1=f\left(x\right)\)
=> y= f(x) là hàm chẵn
b) Xét tính đồng biến, nghịch biến
Với mọi \(x_1>x_2\)
\(f\left(x_1\right)-f\left(x_2\right)=\left(x_1^2+2\left|x_1\right|-1\right)-\left(x_2^2+2\left|x_2\right|-1\right)\)
\(=\left(x_1^2-x_2^2\right)+2\left(\left|x_1\right|-\left|x_2\right|\right)\)
+) \(x_1;x_2\in\left(0;+\infty\right)\)
\(f\left(x_1\right)-f\left(x_2\right)=\left(x_1^2-x_2^2\right)+2\left(x_1-x_2\right)=\left(x_1-x_2\right)\left(x_1+x_2+2\right)>0\)
=> \(f\left(x_1\right)>f\left(x_2\right)\)
=> Hàm số đồng biến trên \(\left(0;+\infty\right)\)
+) \(x_1;x_2\in\left(-\infty;0\right)\)
\(f\left(x_1\right)-f\left(x_2\right)=\left(x_1^2-x_2^2\right)+2\left(-x_1+x_2\right)=\left(x_1-x_2\right)\left(x_1+x_2-2\right)< 0\)
=> \(f\left(x_1\right)< f\left(x_2\right)\)
> Hàm số nghịch biến trên \(\left(-\infty;0\right)\)
2.
\(y=f\left(x\right)=x+\frac{1}{x}\)
TXD: D=R\{0}
a) Xét tính chẵn lẻ.
Với mọi x thuộc D => -x thuộc D
Có \(f\left(-x\right)=-x+\frac{1}{-x}=-\left(x+\frac{1}{x}\right)=-f\left(x\right)\)
=> y= f(x) là hàm lẻ
Em tự làm tiếp nhé. Tương tự như trên

4A
5. \(\left\{{}\begin{matrix}a+b+2=5\\4a-2b+2=8\end{matrix}\right.\) \(\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\) \(\Rightarrow y=2x^2+x+2\)
6. \(\left\{{}\begin{matrix}-\frac{b}{2a}=-2\\\frac{4ac-b^2}{4a}=4\\c=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=4a\\24a-16a^2=16a\\c=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\frac{1}{2}\\b=2\\c=6\end{matrix}\right.\) \(\Rightarrow y=\frac{1}{2}x^2+2x+6\)
7. \(\left\{{}\begin{matrix}c=-1\\a+b+c=-1\\a-b+c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-1\\c=-1\end{matrix}\right.\) \(\Rightarrow y=x^2-x-1\)
8.
a/ \(AM=\sqrt{2}\)
b/ \(AM=\sqrt{10}\)
c/ Không thuộc đồ thị
d/ Không thuộc đồ thị
Đáp án A đúng
Đáp án A