Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

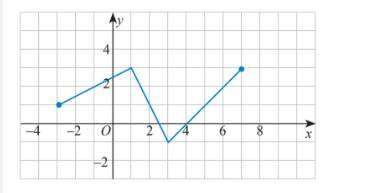
a) Từ đồ thị ta thấy hàm số xác định trên [-3;7]
+) Trên khoảng (-3; 1): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
+) Trên khoảng (1; 3): đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
+) Trên khoảng (3; 7): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).
b) Xét hàm số \(y = 5{x^2}\) trên khoảng (2; 5).
Lấy \({x_1},{x_2} \in (2;5)\) là hai số tùy ý sao cho \({x_1} < {x_2}\).
Do \({x_1},{x_2} \in (2;5)\) và \({x_1} < {x_2}\) nên \(0 < {x_1} < {x_2}\), suy ra \({x_1}^2 < {x_2}^2\) hay \(5{x_1}^2 < 5{x_2}^2\)
Từ đây suy ra \(f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).

a) hệ số a=-2=>y luôn nghịch biến
b) a=1 >0 và -b/2a =-5 => (-5;+vc) y luôn đồng biến
c) hàm y có dạng y=a/(x+1)
a =-1 => y đồng biến (-vc;-1) nghich biến (-1;+vc
=>
(-3;-2) hàm y đồng biến
(2;3) hàm y đồng biến
a) Hàm số \(y=-2x+3\) có a = -2 < 0 nên hàm số nghịch biến trên R.
b. Xét tỉ số \(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\left(x^2_1+10x_1+9\right)-\left(x^2_2+10x_2+9\right)}{x_1-x_2}\)
\(=\dfrac{\left(x_1-x_2\right)\left(x_1+x_2+10\right)}{x_1-x_2}=x_1+x_2+10\).
Với \(x_1;x_2\notin\left(-5;+\infty\right)\) thì \(x_1+x_2+10\ge0\) nên hàm số y đồng biến trên \(\left(-5;+\infty\right)\).
c) Xét tỉ số: \(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{-\dfrac{1}{x_1+1}+\dfrac{1}{x_2+1}}{x_1-x_2}=\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}\)
Trên \(\left(-3;-2\right)\) thì \(\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}< 0\) nên hàm số y nghịch biến trên \(\left(-3;-2\right)\).
Trên \(\left(2;3\right)\) thì \(\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}>0\) nên hàm số y đồng biến trên \(\left(2;3\right)\).

a) Đk:\(x\in R\)
TH1:Xét \(x\in\left(3;+\infty\right)\)
Lấy \(x_1;x_2\in\left(3;+\infty\right)\) thỏa mãn \(x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{2x_1^2-4x_1+3-\left(2x_2^2-4x_2+3\right)}{x_1-x_2}\)\(=2\left(x_1+x_2\right)-4\)
Do \(x_1;x_2\in\left(3;+\infty\right)\)\(\Rightarrow2\left(x_1+x_2\right)>12\Leftrightarrow2\left(x_1+x_2\right)-4>8>0\)
\(\Rightarrow I>0\)
Hàm đồng biến trên \(\left(3;+\infty\right)\)
TH2:Xét \(x\in\left(-10;1\right)\)
Lấy \(x_1;x_2\in\left(-10;1\right):x_1\ne x_2\)
Xét \(I=2\left(x_1+x_2\right)-4\)
Do \(x_1< 1;x_2< 1\Rightarrow2\left(x_1+x_2\right)< 4\Rightarrow I=2\left(x_1+x_2\right)-4< 0\)
Hàm nb trên khoảng \(\left(-10;1\right)\)
b)Làm tương tự,hàm nb trên \(\left(1;+\infty\right)\) và đb trên \(\left(-10;-2\right)\)
c)Đk: \(x\in R\backslash\left\{2\right\}\)
=>Hàm số xác định trên \(\left(-\infty;2\right)\)
Lấy \(x_1;x_2\in\left(-\infty;2\right):x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\dfrac{x_1}{x_1-2}-\dfrac{x_2}{x_2-2}}{x_1-x_2}=\dfrac{-2}{\left(x_1-2\right)\left(x_2-2\right)}\)
Do \(x_1;x_2< 2\Rightarrow\left(x_1-2\right)\left(x_2-2\right)>0\)
\(\Rightarrow I=-\dfrac{2}{\left(x_1-2\right)\left(x_2-2\right)}< 0\)
Hàm nb trên \(\left(-\infty;2\right)\)
d)\(I=\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}\)
Hàm đb trên \(\left(-1;+\infty\right)\) ; \(\left(-3;-2\right)\)
e)TXĐ:D=R
Lấy \(x_1;x_2\in\left(0;+\infty\right):x_1< x_2\)
\(T=f\left(x_1\right)-f\left(x_2\right)=x_1^{2020}+x_1^2-3-x_2^{2020}-x_2^2+3=x_1^{2020}-x_2^{2020}+x_1^2-x_2^2\)
Do \(x_1< x_2\Rightarrow x_1^{2020}< x_2^{2020};x_1^2< x_2^2\)
\(\Rightarrow T=x_1^{2020}-x_2^{2020}+x_1^2-x_2^2< 0\)
Hàm đb trên \(\left(0;+\infty\right)\)
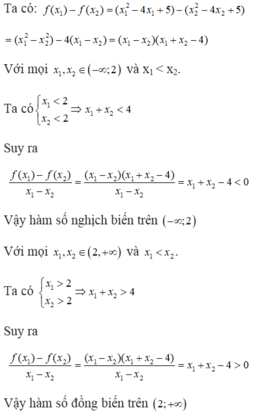
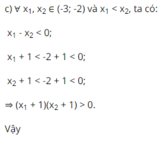

làm luôn nha :
a) đặc : \(f\left(x\right)=y=-x^2-4x-5\)
ta chọn \(a=-3;b=-4\) thuộc \(\left(-\infty;-2\right)\)
\(\Rightarrow\dfrac{f\left(a\right)-f\left(b\right)}{a-b}=\dfrac{-\left(-3\right)^2-4\left(-3\right)-5-\left(-\left(-4\right)^2-4\left(-4\right)-5\right)}{-3-\left(-4\right)}=3\)
\(\Rightarrow\) hàm số này đồng biến .
b) đặc \(f\left(x\right)=y=\dfrac{x+2}{x-1}\)
ta chọn \(a=-1;b=0\) thuộc \(\left(-\infty;1\right)\)
\(\Rightarrow\dfrac{f\left(a\right)-f\left(b\right)}{a-b}=\dfrac{\dfrac{-1+2}{-1-1}-\dfrac{0+2}{0-1}}{-1}=\dfrac{-3}{2}\)\(\Rightarrow\) hàm số này nghịch biến .
làm cách không chọn giá trị theo yc :
a) đặc : \(f\left(x\right)=y=-x^2-4x-5\)
giả sử : \(a< b< -2\)
khi đó ta có : \(\dfrac{f\left(a\right)-f\left(b\right)}{a-b}=\dfrac{-a^2-4a-5-\left(-b^2-4b-5\right)}{a-b}\)
\(\dfrac{b^2-a^2+4b-4a}{a-b}=\dfrac{\left(b-a\right)\left(a+b\right)+4\left(b-a\right)}{a-b}\)
\(=\dfrac{-\left(a+b+4\right)\left(a-b\right)}{a-b}=-\left(a+b+4\right)\)
vì \(a< b< -2\Rightarrow a+b< -4\Rightarrow a+b+4< 0\Rightarrow-\left(a+b+4\right)>0\)
\(\Rightarrow\) hàm số đồng biến
b) đặc : \(f\left(x\right)=y=\dfrac{x+2}{x-1}\)
giả sử : \(a< b< 1\)
khi đó ta có : \(\dfrac{f\left(a\right)-f\left(b\right)}{a-b}=\dfrac{\dfrac{a+2}{a-1}-\dfrac{b+2}{b-1}}{a-b}\)
\(\dfrac{\dfrac{3b-3a}{\left(a-1\right)\left(b-1\right)}}{a-b}=\dfrac{3\left(b-a\right)}{\left(a-1\right)\left(b-1\right)\left(a-b\right)}\)
\(=\dfrac{-3}{\left(a-1\right)\left(b-1\right)}\)
vì \(a< b< 1\Rightarrow\left(a-1\right);\left(b-1\right)< 0\) \(\Rightarrow\left(a-1\right)\left(b-1\right)>0\)
\(\Rightarrow\dfrac{-3}{\left(a-1\right)\left(b-1\right)}< 0\)
\(\Rightarrow\) hàm số nghịch biến