tìm hai số tự nhiên x y biết rằng bcnn (x,y) = 90 và x.y= 1350
Có ai giúp mình đi, làm ơn🥺🥺
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 7 2021
Áp dụng tính chất dãy tỉ số bằng nhau có:
x/2=y/3=x.y/2.3=216/6=36
x/2=36
x=72
y/3=36
y=108
B
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 12 2022
X - { [ -x + (x+3) ] } - [ (x+3) - (x-2)] = 0
X - { -x + x + 3 } - [ x +3 - x +2] = 0
X - 3 - 5 = 0
x - 8 = 0
x = 8
NH
3
BD
9 tháng 12 2016
Vì ƯCLN(x,y) = 10, suy ra : x = 10a ; y = 10b
(với a <b và ƯCLN(a;b) = 1 )
Ta có : x.y = 10a . 10b = 100ab (1)
Mặt khác:x.y = ƯCLN(x;y). BCNN(x;y)
x.y = 10 . 900 = 9000 (2)
Từ (1) và (2), suy ra: ab = 90
Ta có các trường hợp sau:
y | 1 | 2 | 3 | 5 | 9 |
a | 90 | 45 | 30 | 18 | 10 |
Từ đó suy ra và b có các trường hợp sau:
b | 10 | 20 | 30 | 50 | 90 |
x | 900 | 450 | 300 | 180 | 100 |
PT
1
CM
28 tháng 10 2019
- Đặt (x; y) = d nên x = d.m; y = d.n với (m;n) =1. Giả sử x ≤ y thì m ≤ n.
- Ta có: x.y = dm.dn= d2.mn
BCNN(x; y) = x y x ; y = d 2 m . n d = d . m . n
- Ta có: BCNN (x;y) = 10 và x. y = 20 nên d = x y B C N N ( x ; y ) = 20 10 = 2
=> 2.m.n =10 nên m.n = 5
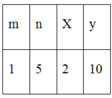
Bảng giá trị
DK
0
F
1
30 tháng 10 2018
\(ƯCLN\left(x;y\right)=\frac{xy}{BCNN\left(x;y\right)}=\frac{20}{10}=2\)
Đặt \(x=2k,y=2t\) (y và t là 2 số nguyên tố cùng nhau)
\(xy=20\Rightarrow2k.2t=20\Rightarrow k.t=5\)
\(\Rightarrow k\inƯ\left(5\right)=\left\{1;5\right\}\)
\(\Rightarrow x=2k\in\left\{2;10\right\}\)
Nếu x = 2 thì y = 10
Nếu x = 10 thì y = 2
Vậy x = 2 và y = 10 hoặc x = 10 và y = 2
Giả sử x>y ta có :
\(\hept{\begin{cases}90=2\cdot3^2\cdot5\\1350=2.3^3.5^2\end{cases}}\)
vậy ta có hai số (x,y) là \(\hept{\begin{cases}x=3^2\cdot5\\y=2\cdot3\cdot5\end{cases}\text{ hoặc :}\hept{\begin{cases}x=2\cdot3^2\cdot5\\y=3\cdot5\end{cases}}}\)
tương tự với y>x