Question

[Bảo Việt]

1) Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y=x⁴- mx² đồng biến trên khoảng (2;+\(\infty\))

2) Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn của số phức z thỏa mãn 1\(\le\) \(\left|z\right|\)\(\le\)2 là một hình phẳng có diện tích bằng ?

3) Gọi z là số phức có modun nhỏ nhất thỏa mãn \(\left|z+i+1\right|\) = \(\left|z+i\right|\) (vế phải là z gạch đầu nha :D)

4) Trong không gian Oxyz, cho tam giác ABC có điểm C(3;2;3), đường cao qua A, B lần lượt là d₁: \(\frac{x-2}{1}\)= \(\frac{y-3}{1}\)=\(\frac{z-3}{-2}\); d₂: \(\frac{x-1}{1}\)=\(\frac{y-4}{-2}\)= \(\frac{z-3}{1}\). Hoành độ điểm A là ?

Answer 1

[Nguyễn Việt Lâm]

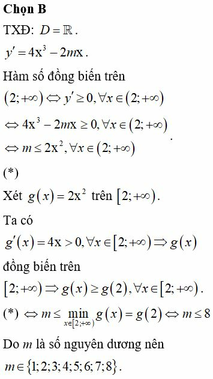
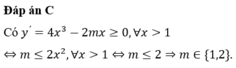
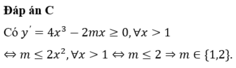
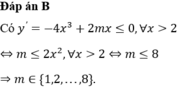
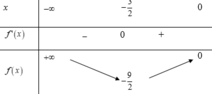
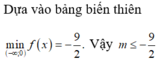
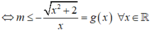
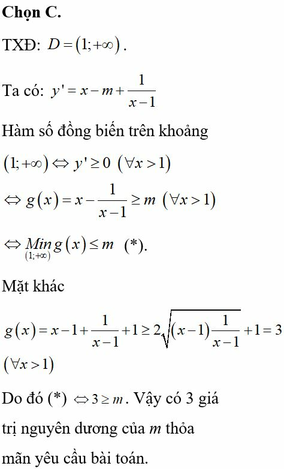
a/ \(y'=4x^3-2mx=2x\left(2x^2-m\right)\)

Do \(a=1>0\Rightarrow\)nếu \(m>0\Rightarrow\) hàm số có 1 khoảng đồng biến là \(\left(\sqrt{\frac{m}{2}};+\infty\right)\)

\(\Rightarrow\sqrt{\frac{m}{2}}\le2\Rightarrow0< m\le8\)

Vậy \(m\le8\) \(\Rightarrow\) có 8 giá trị nguyên dương

Bài 2:

\(1\le\sqrt{a^2+b^2}\le2\Rightarrow1\le a^2+b^2\le4\)

\(\Rightarrow\) Tập hợp \(z\) là hình vành khuyên giới hạn bởi 2 đường tròn có tâm là gốc tọa độ và bán kính lần lượt là 1 và 2

\(\Rightarrow S=\pi.2^2-\pi.1^2=3\pi\)

Bài 3: Không thấy câu hỏi đâu hết, chỉ thấy gọi số phức z mà ko thấy yêu cầu làm gì với nó cả :(

Bài 4:

Do \(A\in d_1:\left\{{}\begin{matrix}x=2+t\\y=3+t\\z=3-2t\end{matrix}\right.\) \(\Rightarrow A\left(a+2;a+3;3-2a\right)\)

\(\Rightarrow\overrightarrow{CA}=\left(a-1;a+1;-2a\right)\)

Do \(d_2\perp AC\Rightarrow\overrightarrow{CA}.\overrightarrow{u_{d2}}=0\)

\(\Rightarrow1\left(a-1\right)-2\left(a+1\right)+1\left(-2a\right)=0\)

\(\Rightarrow-3a=3\Rightarrow a=-1\)

\(\Rightarrow x_A=a+2=1\)

Answer 2

[Bảo Việt]

à sr nha bạn ghi thiếu..., câu 3 hỏi tổng phần thực và phần ảo bằng bao nhiêu ấy