Giúp mình bài này với ạ, ghi rõ cả dkxd ra nha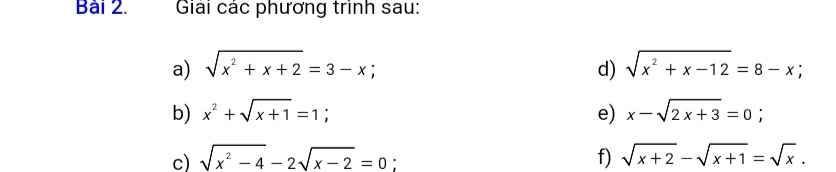
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Ta có: \(\sqrt{3x-5}=2\)
\(\Leftrightarrow3x-5=4\)
hay x=3
2: Ta có: \(\sqrt{25\left(x-1\right)}=20\)
\(\Leftrightarrow x-1=16\)
hay x=17

\(ĐK:x\ne0;2\)
\(\Leftrightarrow\dfrac{x+2}{x}-\dfrac{2x+3}{2\left(x-2\right)}=0\)
\(\Leftrightarrow\dfrac{2\left(x-2\right)\left(x+2\right)-x\left(2x+3\right)}{2x\left(x-2\right)}=0\)
\(\Leftrightarrow2\left(x^2-4\right)-x\left(2x+3\right)=0\)
\(\Leftrightarrow2x^2-8-2x^2-3x=0\)
\(\Leftrightarrow-3x=8\Leftrightarrow x=-\dfrac{8}{3}\left(tm\right)\)

ĐKXĐ:\(x\ne\pm1\)
\(\dfrac{x-1}{x+1}-\dfrac{x+1}{x-1}=\dfrac{14}{x^2-1}\\ \Leftrightarrow\dfrac{\left(x-1\right)^2}{\left(x+1\right)\left(x-1\right)}-\dfrac{\left(x+1\right)^2}{\left(x+1\right)\left(x-1\right)}-\dfrac{14}{\left(x+1\right)\left(x-1\right)}=0\\ \Rightarrow x^2-2x+1-x^2-2x-1-14=0\\ \Leftrightarrow-4x-14=0\\ \Leftrightarrow x=-\dfrac{7}{2}\left(tm\right)\)

\(\Leftrightarrow\dfrac{3\left(2x-1\right)-36}{12}=\dfrac{2\left(1+x\right)}{12}\)
\(\Leftrightarrow\dfrac{6x-3-36}{12}=\dfrac{2+2x}{12}\)
\(\Leftrightarrow6x-39=2+2x\)
\(\Leftrightarrow4x=41\Leftrightarrow x=\dfrac{41}{4}\)

\(\left(2-x\right)^2=\left(2x-1\right)\left(2x+1\right)\\ \Leftrightarrow4-4x+x^2=4x^2-1\\ \Leftrightarrow4x^2-1-x^2+4x-4=0\\ \Leftrightarrow3x^2+4x-5=0\)
Đến đây mik thấy nghiệm rất xấu bạn xem đề đúng chx nhé

\(\left(2x-5\right)\left(x-7\right)=\left(x-7\right)\left(5+x\right)\\ \Leftrightarrow\left(2x-5\right)\left(x-7\right)-\left(x-7\right)\left(5+x\right)=0\\ \Leftrightarrow\left(x-7\right)\left(2x-5-5-x\right)=0\\ \Leftrightarrow\left(x-7\right)\left(x-10\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-7=0\\x-10=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=7\\x=10\end{matrix}\right.\)
\(\left(2x-5\right)\left(x-7\right)-\left(x-7\right)\left(5+x\right)=0\\ \left(x-7\right)\left(2x-5-5-x\right)=0\\ \left(x-7\right)\left(x-10\right)=0\\ \left\{{}\begin{matrix}x-7=0\\x-10=0\end{matrix}\right.\left\{{}\begin{matrix}x=7\\x=10\end{matrix}\right.\)

\(Đk:x\ne0;3\)
\(\Leftrightarrow\dfrac{x+3}{x-3}=\dfrac{18}{x\left(x-3\right)}+\dfrac{8}{x}\)
\(\Leftrightarrow\dfrac{x\left(x+3\right)}{x\left(x-3\right)}=\dfrac{18+8\left(x-3\right)}{x\left(x-3\right)}\)
\(\Leftrightarrow x^2+3x=18+8x-24\)
\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(ktm\right)\\x=2\left(tm\right)\end{matrix}\right.\)

Bài 4:
\(a,A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\\ P=A:B=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{x-1}{\sqrt{x}+1}=\dfrac{x-1}{\sqrt{x}}\\ b,P\sqrt{x}=m-\sqrt{x}+x\\ \Leftrightarrow x-1=m-\sqrt{x}+x\\ \Leftrightarrow m=\sqrt{x}-1\)

\(a,ĐK:x\le2\\ PT\Leftrightarrow x^2-x-8=4-2x\Leftrightarrow x^2+x-12=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(ktm\right)\\x=-4\left(tm\right)\end{matrix}\right.\Leftrightarrow x=-4\\ b,ĐK:5x^2+10x+1\ge0\\ PT\Leftrightarrow5x^2+10x+1=\left(7-x^2-2x\right)^2\\ \Leftrightarrow5x^2+10x+1=x^4+4x^2+49-14x^2+4x^3-28x\\ \Leftrightarrow x^4+4x^3-15x^2-38x+48=0\\ \Leftrightarrow x^4-x^3+5x^3-5x^2-10x^2+10x-48x+48=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+5x^2-10x-48\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+3x^2+2x^2+6x-16x-48\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+3\right)\left(x^2+2x-16\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\\x^2+2x-16=0\left(1\right)\end{matrix}\right.\)
\(\Delta\left(1\right)=4+64=68\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-2-2\sqrt{17}}{2}=-1-\sqrt{17}\\x=\dfrac{-2+2\sqrt{17}}{2}=-1+\sqrt{17}\end{matrix}\right.\)
Vậy pt có nghiệm ...



a. ĐKXĐ: $x\in\mathbb{R}$
PT \(\Rightarrow \left\{\begin{matrix} 2-x\geq 0\\ x^2+x+2=(3-x)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 2\\ x^2+x+2=x^2-6x+9\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\leq 2\\ 7x=7\end{matrix}\right.\Leftrightarrow x=1\)
b. ĐKXĐ: $x\geq -1$
PT $\Leftrightarrow (x^2-1)+\sqrt{x+1}=0$
$\Leftrightarrow (x-1)(x+1)+\sqrt{x+1}=0$
$\Leftrightarrow \sqrt{x+1}[(x-1)\sqrt{x+1}+1]=0$
$\Leftrightarrow \sqrt{x+1}=0$ hoặc $(x-1)\sqrt{x+1}+1=0$
Nếu $\sqrt{x+1}=0$
$\Leftrightarrow x=-1$ (tm)
Nếu $(x-1)\sqrt{x+1}+1=0$
$\Leftrightarrow (x-1)\sqrt{x+1}=-1$
$\Rightarrow (x-1)^2(x+1)=1$
$\Leftrightarrow x^3-x^2-x=0$
$\Leftrightarrow x(x^2-x-1)=0$
$\Leftrightarrow x=0$ hoặc $x^2-x-1=0$
$\Leftrightarrow x=0$ hoặc $x=\frac{1\pm \sqrt{5}}{2}$
Kết hợp đkxđ suy ra $x=0; -1; \frac{1\pm \sqrt{5}}{2}$
c. ĐKXĐ: $x\geq 2$
PT $\Leftrightarrow \sqrt{(x-2)(x+2)}-2\sqrt{x-2}=0$
$\Leftrightarrow \sqrt{x-2}(\sqrt{x+2}-2)=0$
$\Leftrightarrow \sqrt{x-2}=0$ hoặc $\sqrt{x+2}-2=0$
$\Leftrightarrow x=2$ (thỏa mãn)
d. ĐKXĐ: $x\geq 3$ hoặc $x\leq -4$
PT \(\Rightarrow \left\{\begin{matrix} 8-x\geq 0\\ x^2+x-12=(8-x)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 8\\ x^2+x-12=x^2-16x+64\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\leq 8\\ 17x=76\end{matrix}\right.\Leftrightarrow x=\frac{76}{17}\) (tm)