
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. ĐKXĐ: $x\in\mathbb{R}$
PT \(\Rightarrow \left\{\begin{matrix} 2-x\geq 0\\ x^2+x+2=(3-x)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 2\\ x^2+x+2=x^2-6x+9\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\leq 2\\ 7x=7\end{matrix}\right.\Leftrightarrow x=1\)
b. ĐKXĐ: $x\geq -1$
PT $\Leftrightarrow (x^2-1)+\sqrt{x+1}=0$
$\Leftrightarrow (x-1)(x+1)+\sqrt{x+1}=0$
$\Leftrightarrow \sqrt{x+1}[(x-1)\sqrt{x+1}+1]=0$
$\Leftrightarrow \sqrt{x+1}=0$ hoặc $(x-1)\sqrt{x+1}+1=0$
Nếu $\sqrt{x+1}=0$
$\Leftrightarrow x=-1$ (tm)
Nếu $(x-1)\sqrt{x+1}+1=0$
$\Leftrightarrow (x-1)\sqrt{x+1}=-1$
$\Rightarrow (x-1)^2(x+1)=1$
$\Leftrightarrow x^3-x^2-x=0$
$\Leftrightarrow x(x^2-x-1)=0$
$\Leftrightarrow x=0$ hoặc $x^2-x-1=0$
$\Leftrightarrow x=0$ hoặc $x=\frac{1\pm \sqrt{5}}{2}$
Kết hợp đkxđ suy ra $x=0; -1; \frac{1\pm \sqrt{5}}{2}$
c. ĐKXĐ: $x\geq 2$
PT $\Leftrightarrow \sqrt{(x-2)(x+2)}-2\sqrt{x-2}=0$
$\Leftrightarrow \sqrt{x-2}(\sqrt{x+2}-2)=0$
$\Leftrightarrow \sqrt{x-2}=0$ hoặc $\sqrt{x+2}-2=0$
$\Leftrightarrow x=2$ (thỏa mãn)
d. ĐKXĐ: $x\geq 3$ hoặc $x\leq -4$
PT \(\Rightarrow \left\{\begin{matrix} 8-x\geq 0\\ x^2+x-12=(8-x)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 8\\ x^2+x-12=x^2-16x+64\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\leq 8\\ 17x=76\end{matrix}\right.\Leftrightarrow x=\frac{76}{17}\) (tm)

1: Ta có: \(\sqrt{3x-5}=2\)
\(\Leftrightarrow3x-5=4\)
hay x=3
2: Ta có: \(\sqrt{25\left(x-1\right)}=20\)
\(\Leftrightarrow x-1=16\)
hay x=17

\(A=\frac{1}{1-\sqrt{a}}+\frac{a\sqrt{a}}{\sqrt{a}-1}\left(a\ge0,a\ne1\right)\)
\(A=\frac{-1}{\sqrt{a}-1}+\frac{a\sqrt{a}}{\sqrt{a}-1}\)
\(A=\frac{-1+a\sqrt{a}}{\sqrt{a}-1}=\frac{a\sqrt{a}-1}{\sqrt{a}-1}\)
\(A=\frac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}-1}\)
\(A=\frac{a+\sqrt{a}+1}{1}=a+\sqrt{a}+1\)
Vậy.............
-Chúc bạn học tốt >.<-
_Minh ngụy_

-tham khảo tại bài mà mình đã giải tại đây-
Câu hỏi của Trần Nam Hải - Toán lớp 9 - Học toán với OnlineMath
https://olm.vn/hoi-dap/detail/228029923283.html
- Chúc bạn học tốt -
_Minh ngụy_
\(A=\frac{1}{1-\sqrt{a}}+\frac{a\sqrt{a}}{\sqrt{a}-1}\left(\text{ĐKXĐ: a}\ne1\right)\)
\(A=\frac{-1}{-\left(1-\sqrt{a}\right)}+\frac{\left(\sqrt{a}\right)^2.\sqrt{a}}{\sqrt{a}-1}\)
\(A=\frac{-1}{\sqrt{a}-1}+\frac{\sqrt{a}^3}{\sqrt{a}-1}\)
\(A=\frac{-1+\sqrt{a}^3}{\sqrt{a}-1}\)
\(A=\frac{\sqrt{a}^3-1}{\sqrt{a}-1}\)
\(A=\frac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}-1}\)
\(A=a+\sqrt{a}+1\)

\(\dfrac{x+2}{x-2}-\dfrac{2}{x^2-2x}=\dfrac{1}{x}\)
\(\Leftrightarrow\dfrac{x+2}{x-2}-\dfrac{2}{x\left(x-2\right)}=\dfrac{1}{x}\)
ĐKXĐ:\(\left\{{}\begin{matrix}x\ne0\\x\ne2\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{x\left(x+2\right)}{x\left(x-2\right)}-\dfrac{2}{x\left(x-2\right)}=\dfrac{x-2}{x\left(x-2\right)}\)
\(\Leftrightarrow x^2+2x-2=x-2\)
\(\Leftrightarrow x^2+x=0\Leftrightarrow x\left(x+1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\left(kTM\right)\\x=-1\left(TM\right)\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm \(x=-1\)
Ta có: \(\dfrac{x+2}{x-2}-\dfrac{2}{x^2-2x}=\dfrac{1}{x}\)
\(\Leftrightarrow x\left(x+2\right)-2=x-2\)
\(\Leftrightarrow x^2+2x-x=0\)
\(\Leftrightarrow x\left(x+1\right)=0\)
hay x=-1

Ta có: \(\dfrac{3}{1-x^2}-\dfrac{1}{x+1}=\dfrac{2}{x^3-x^2-x+1}\)
\(\Leftrightarrow\dfrac{-3}{\left(x-1\right)\left(x+1\right)}-\dfrac{x-1}{\left(x+1\right)\left(x-1\right)}=\dfrac{2}{\left(x-1\right)^2\cdot\left(x+1\right)}\)
\(\Leftrightarrow\dfrac{-\left(x+2\right)\left(x-1\right)}{\left(x-1\right)^2\cdot\left(x+1\right)}=\dfrac{2}{\left(x-1\right)^2\cdot\left(x+1\right)}\)
\(\Leftrightarrow-\left(x^2-x+2x-2\right)=2\)
\(\Leftrightarrow x^2+x-2=-2\)
\(\Leftrightarrow x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
Vậy: S={0}

ta có: \(x\sqrt{5}-x^2+2=-\left(x^2-x\sqrt{5}\right)+2=-\left(x^2-2.x.\frac{\sqrt{5}}{2}+\frac{5}{4}\right)+\frac{5}{4}+2\)
\(=-\left(x-\frac{\sqrt{5}}{2}\right)^2+\frac{13}{4}\)
Mà \(\left(x-\frac{\sqrt{5}}{2}\right)^2\ge0\) với mọi x
nên \(-\left(x-\frac{\sqrt{5}}{2}\right)^2+\frac{13}{4}\le\frac{13}{4}\)
\(\Rightarrow x\sqrt{5}-x^2+2\le\frac{13}{4}\)
=> GTLN của \(x\sqrt{5}-x^2+2\) là 13/4 <=> \(x-\frac{\sqrt{5}}{2}=0\Leftrightarrow x=\frac{\sqrt{5}}{2}\)

có 9 trang đánh bằng 1 chữ số: Từ trang 1 đến trang 9
Có 90 trang đánh số từ trang 10 đến 99
Vậy có 9 trang đánh bằng 3 chữ số: Từ 100 đến 108
Có 108 trang sách


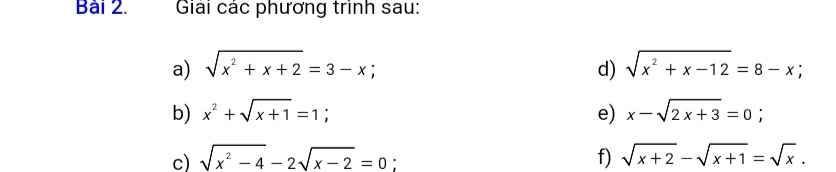

\(a,ĐK:x\le2\\ PT\Leftrightarrow x^2-x-8=4-2x\Leftrightarrow x^2+x-12=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(ktm\right)\\x=-4\left(tm\right)\end{matrix}\right.\Leftrightarrow x=-4\\ b,ĐK:5x^2+10x+1\ge0\\ PT\Leftrightarrow5x^2+10x+1=\left(7-x^2-2x\right)^2\\ \Leftrightarrow5x^2+10x+1=x^4+4x^2+49-14x^2+4x^3-28x\\ \Leftrightarrow x^4+4x^3-15x^2-38x+48=0\\ \Leftrightarrow x^4-x^3+5x^3-5x^2-10x^2+10x-48x+48=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+5x^2-10x-48\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+3x^2+2x^2+6x-16x-48\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+3\right)\left(x^2+2x-16\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\\x^2+2x-16=0\left(1\right)\end{matrix}\right.\)
\(\Delta\left(1\right)=4+64=68\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-2-2\sqrt{17}}{2}=-1-\sqrt{17}\\x=\dfrac{-2+2\sqrt{17}}{2}=-1+\sqrt{17}\end{matrix}\right.\)
Vậy pt có nghiệm ...