Khi cung cấp cho vật khối lượng m1 vận tốc ban đầu v1 = 4m/s thì nó sẽ
trượt được đoạn đường dài 2m trên mặt phẳng ngang rồi dừng lại do có ma sát. Nếu
cung cấp cho vật khối lượng m2 = 2m1 vận tốc ban đầu v2 = 6m/s để m2 cũng trượt trên
mặt phẳng ngang đó thì khi dừng lại m2 đã trượt được đoạn đường bằng:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
14 tháng 1 2020
biến thiên động năng \(\left(v1=0\right)\)
\(A.F_{ms}=\frac{1}{2}.m1.\left(v\overset{2}{1'}-v\overset{2}{1}\right)\)
\(\Rightarrow F_{ms}.s.\cos180^o=-8.m1\)
\(\Rightarrow F_{ms}=4m1\)
đối với mật m2=2m1
biến thiên động năng (v2'=0)
\(A.F_{ms}=\frac{1}{2}.m2.\left(v\overset{2}{2'}-v\overset{2}{2}\right)\)
\(\Leftrightarrow4m1.s.\cos180^o=m1.\left(-36\right)\)
\(\Leftrightarrow s=9m\)
14 tháng 1 2020
Khi cung cấp cho vật kl m1 vận tốc ban đầu v1 =4m/s thì nó sẽ trượt đc đoạn đường dài 2 m trên mặt phẳng nằm ngang rồi dừng lại do có ma sát .Nếu cung cấp vật kl m2 = 2m1 vận tốc ban đầu v2 = 6m/s để m2 cũng trượt trên mặt phẳng đó thì khi dừng lại m2 đã trượt đc đoạn đường bằng bao nhiêu
______________________________
Giải
Khi bắt đầu chuyển động đến khi dừng lại động năng của vật đã chuyển hóa thành công của lực ma sát
\(\left\{{}\begin{matrix}W_{d1}=A_{F_{ms1}}\\W_{d2}=A_{F_{ms2}}\end{matrix}\right.\)
\(\rightarrow\left\{{}\begin{matrix}\frac{1}{2}m_1v_1^2=\mu m_1g .s_1\\\frac{1}{2}m_2v_2^2=\mu.m_2\text{g }.s_1\end{matrix}\right.\)
\(\rightarrow s_1=s_2.\frac{v_2^2}{v_1^2}=2.\frac{6^2}{4^2}=4,5\left(m\right)\)
VT
9 tháng 5 2017
Đáp án: A
Phương trình động lực học:
Chiếu (1) lên phương song song với mặt phẵng nghiêng (phương chuyển động), chiều dương hướng xuống (cùng chiều chuyển động), ta có:
Psina – Fms = ma1
Chiếu (1) lên phương vuông góc với mặt phẵng nghiêng (vuông góc với phương chuyển động), chiều dương hướng lên, ta có:
N - Pcosa = 0
→ N = Pcosa = mgcosa
→ Fms = m1N = m1mgcosa.
Gia tốc trên mặt phẵng nghiêng:
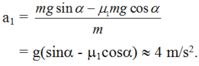
Vận tốc của vật tại B:
Gia tốc của vật trên mặt phẵng ngang:
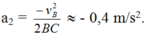
Trên mặt phẵng ngang ta có:
VT
24 tháng 2 2017
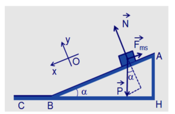
Chọn mốc thế năng tại C (hình 95).
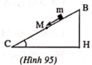
Cơ năng tại B: W B = m g h B
Cơ năng tại M: 
Công của lực ma sát: 
Định luật bảo toàn năng lượng:
30 tháng 11 2021
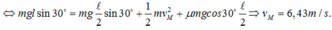
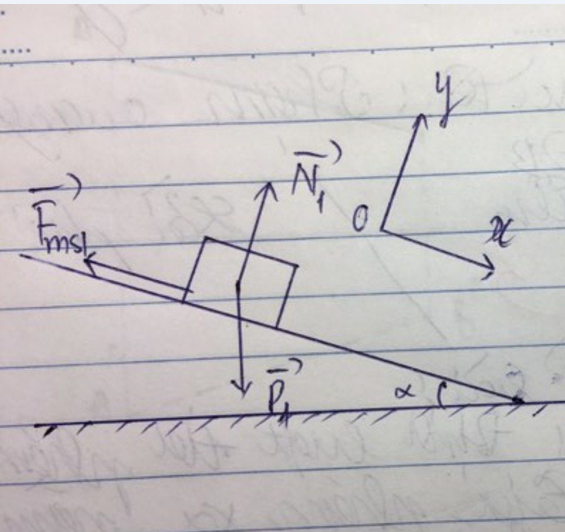
Hình vẽ bạn tham khảo.
Theo định luật ll Niu-tơn ta có:
\(\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
Oy: \(N=P=mg=10m\left(N\right)\)
\(Ox:\) \(-F_{ms}=m\cdot a\)
\(\Rightarrow-\mu mg=m\cdot a\Rightarrow a=-\mu\cdot g=-0,5\cdot10=-5\)m/s2
Quãng đường vật đi:
\(v^2-v^2_0=2aS\Rightarrow S=\dfrac{v^2-v^2_0}{2a}=\dfrac{0-12^2}{2\cdot\left(-5\right)}=14,4m\)
Chọn A.
VT
15 tháng 12 2018
Ta có P 1 x = P 1 . sin 30 0 = m 1 g . 1 2 = 0 , 8.10.0 , 5 = 4 ( N ) P 2 = m 2 g = 0 , 6.10 = 6 ( N )
Vậy P 2 > P 1 x vật hai đi xuống vật một đi lên, khi vật hai đi xuống được một đoạn s = 50 cm thì vật một lên cao
z 1 = s . sin 30 0 = s 2 = 25 ( c m )
Chọn vị trí ban đầu của hai vật là mốc thế năng
Theo định luật bảo toàn năng lượng
0 = W d + W t + A m s V ớ i W d = ( m 1 + m 2 ) v 2 2 = ( 0 , 8 + 0 , 6 ) .1 2 2 = 0 , 7 ( J ) A m s = F m s . s = μ m 1 g . cos 30 0 . s = μ .0 , 8.10. 3 2 .0 , 5 = μ 2 3 ( J )
Vậy 0 = 0 , 7 − 1 + μ .2. 3 ⇒ μ = 0 , 0866
biến thiên động năng (v1'=0)
\(A_{F_{ms}}=\dfrac{1}{2}.m_1.\left(v_{1'}^2-v_1^2\right)\)
\(\Rightarrow F_{ms}.s.cos180^0=\)-8.m1
\(\Rightarrow F_{ms}=4m_1\)
đối với vật m2=2m1
biến thiên động năng(v2'=0)
\(A_{F_{ms}}=\dfrac{1}{2}.m_2.\left(v^2_{2'}-v^2_2\right)\)
\(\Leftrightarrow4m_1.s.cos180^0=m_1.\left(-36\right)\)
\(\Rightarrow s=\)9m