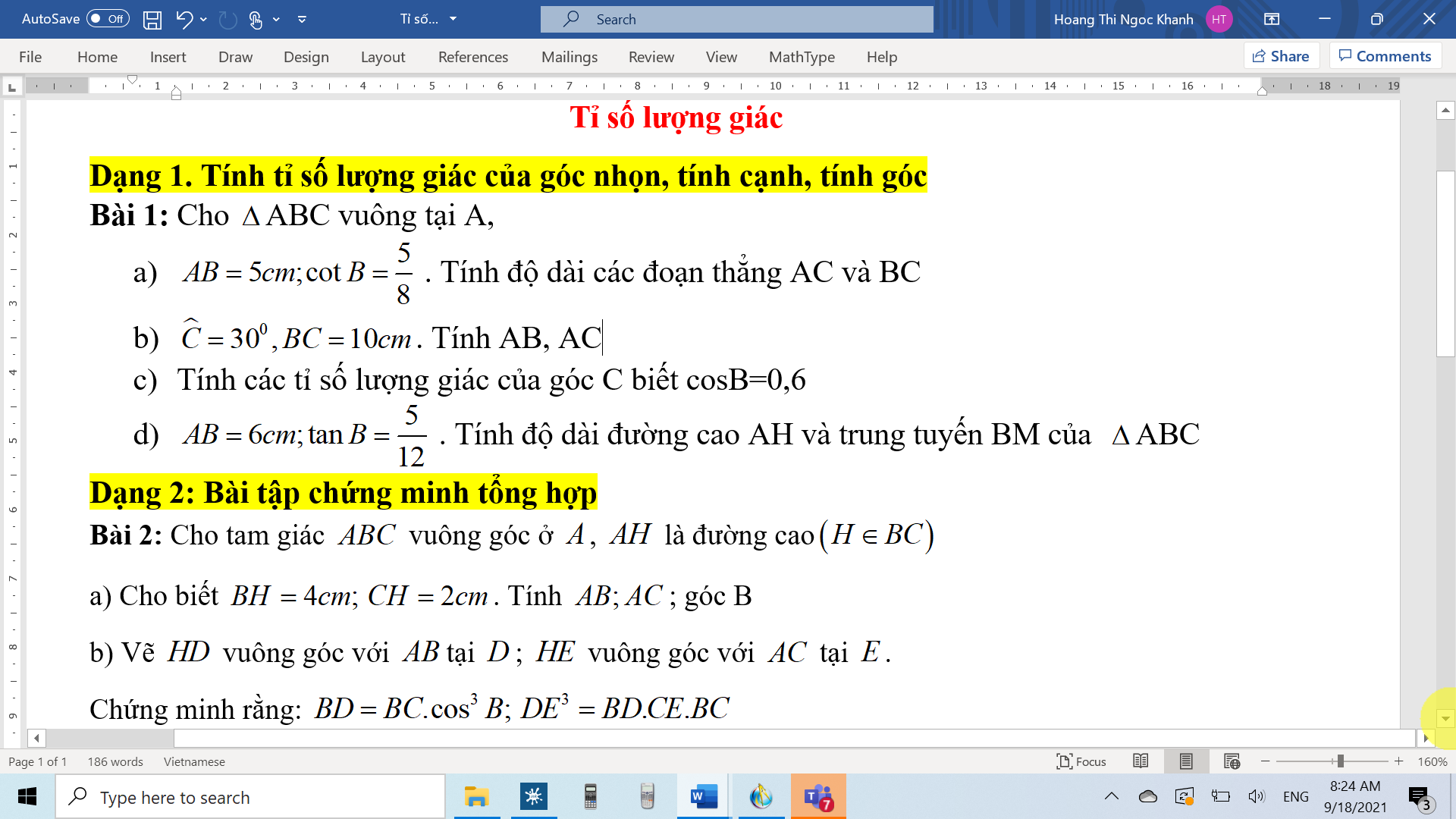
giúp em câu b bài 1 và ý 2 câu b bài 2 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`2)B=(sqrtx+1)/(x-1)-(x+2)/(xsqrtx-1)-(sqrtx+1)/(x+sqrtx+1)(x>0,x ne 1)`
`=(sqrtx+1)/(x-1)-(x+2)/(xsqrtx-1)-(x-1)/(xsqrtx-1)`
`=(sqrtx+1)/(x-1)-(x+2+x-1)/(xsqrtx-1)`
`=(sqrtx+1)/(x-1)-(2x+1)/(xsqrtx-1)`
`=((sqrtx+1)(x+sqrtx+1)-(2x+1)(sqrtx+1))/((x-1)(x-sqrtx+1))`
`=(xsqrtx+2x+2sqrtx+1-2xsqrtx-2x-sqrtx-1)/((x-1)(x-sqrtx+1))`
`=(-xsqrtx+sqrtx)/((x-1)(x-sqrtx+1))`
`=(-sqrtx(x-1))/((x-1)(x-sqrtx+1))`
`=-sqrtx/(x-sqrtx+1)`
Cách khác:
2) Ta có: \(B=\dfrac{\sqrt{x}+1}{x-1}-\dfrac{x+2}{x\sqrt{x}-1}-\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\)
\(=\dfrac{1}{\sqrt{x}-1}-\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\)
\(=\dfrac{x+\sqrt{x}+1-x-2-\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1-x+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{-\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)

Câu 1:
Ta có: \(\left(3x+7\right)\left(2x+3\right)-\left(3x-5\right)\left(2x+11\right)\)
\(=6x^2+9x+14x+21-\left(6x^2+33x-10x-55\right)\)
\(=6x^2+23x+21-6x^2-23x+55\)
=76

\(A=x^6-2x^4-2x^4+4x^2+2x^3-4x\\ A=x^3\left(x^3-2x\right)-2x\left(x^3-2x\right)+2\left(x^3-2x\right)\\ A=\left(x^3-2x\right)\left(x^3-2x+2\right)=3\left(3+2\right)=3\cdot5=15\\ B=x^5-2x^3+3x^3-6x-3x^2\\ =x^2\left(x^3-2x\right)+3\left(x^3-2x\right)-3x^2\\ =\left(x^3-2x\right)\left(x^2+3\right)-3x^2=3\left(x^2+3\right)-3x^2\\ =3x^2-3x^2+9=9\)


`@` `\text {Ans}`
`\downarrow`
`1,`
`a)`
\(\dfrac{x}{2}=\dfrac{y}{3}\text{ và }x+y=50\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2 = y/3 = (x+y)/(2 + 3) = 50/5 = 10`
`=> x/2 = y/3 = 10`
`=> x = 10*2 = 20; y = 3*10 = 30`
Vậy, `x = 20; y = 30`
`b)`
\(\dfrac{x}{2}=\dfrac{y}{3}\text{ và }5x+4y=110\)
Ta có:
`x/2 = y/3` `=> (5x)/10 = (4y)/12`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(5x)/10 = (4y)/12 = (5x+4y)/(10 + 12) = 110/22 = 5`
`=> x/2 = y/3 = 5`
`=> x = 2*5 = 10; y = 3*5 = 15`
Vậy, `x = 10; y = 15`
`c)`
\(5x=11y\text{ và }2x+3y=37\)
Ta có:
`5x = 11y -> x/11 = y/5 -> (2x)/22 = (3y)/15`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(2x)/22 = (3y)/15 = (2x+3y)/(22+15) = 37/37 = 1`
`=> x/11 = y/5 = 1`
`=> x = 11; y = 5`
Vậy, `x = 11; y = 5`
`d)`
\(\dfrac{x}{2}=\dfrac{y}{1}\text{và }x+y-63=0\)
Ta có: `x + y - 63 = 0 -> x + y = 63`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2 = y/1 = (x+y)/(2+1) = 63/3 = 21`
`=> x/2 = y/1 = 21`
`=> x = 21*2 =42; y = 21`
Vậy, `x = 42; y = 21.`
`2,`
`a)`
\(\dfrac{a}{14}=\dfrac{b}{2}=\dfrac{c}{4}\text{ và }a+b+c=5\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`a/14 = b/2 = c/4 = (a+b+c)/(14+2+4)=5/20=1/4=0,25`
`=> a/14 = b/2 = c/4 = 0,25`
`=> a = 14*0,25 = 3,5` `; b = 2*0,25 = 0,5;` `c = 4*0,25 = 1`
Vậy, `a = 3,5`; `b = 0,5`; `c = 1`
`b)`
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{8}\text{ và }7a+3b-5c=7\)
Ta có:
`a/3 = b/5 = c/8 => (7a)/21 = (3b)/15 = (5c)/40`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(7a)/21 = (3b)/15 = (5c)/40 = (7a + 3b - 5c)/(21 + 15 - 40)=7/-4 = -1,75`
`=> a/3 = b/5 = c/8 = -1,75`
`=> a = 3*(-1,75) = -5,25`
`b = 5*(-1,75) = -8,75`
`c = 8*(-1,75) = -14`
Vậy, `a = -5,25; b = -8,75`; `c = -14`
`c)`
\(\dfrac{a}{3}=\dfrac{b}{8}=\dfrac{c}{5}\text{và }3a+b-2c=14\)
Ta có:
`a/3 = b/8 = c/5 -> (3a)/9 = b/8 = (2c)/10`
Câu này bạn làm tương tự nha
`d)`
\(\dfrac{a}{3}=\dfrac{b}{2};\dfrac{b}{7}=\dfrac{c}{5}\text{ và }3a+5c-7b=30\)
Ta có:
`a/3 = b/2 -> a/21 = b/14`/
`b/7 = c/5 -> b/14 = c/10`
`=> a/21 = b/14 = c/10`
`=> (3a)/63 = (7b)/98 = (5c)/50`
Câu này bạn cũng làm tương tự.


1.
d, ĐK: \(x\ge-5\)
\(x-2-4\sqrt{x+5}=-10\)
\(\Leftrightarrow x+5-4\sqrt{x+5}+3=0\)
\(\Leftrightarrow\left(\sqrt{x+5}-1\right)\left(\sqrt{x+5}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+5}=1\\\sqrt{x+5}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=1\\x+5=9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=4\end{matrix}\right.\)
\(\Leftrightarrow x=\pm4\left(tm\right)\)
2.
ĐK: \(x\in R\)
\(\sqrt{x^2+2x+1}+\sqrt{x^2-4x+4}=3\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-2\right)^2}=3\)
\(\Leftrightarrow\left|x+1\right|+\left|x-2\right|=3\)
Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\).
\(\left|x+1\right|+\left|x-2\right|=\left|x+1\right|+\left|2-x\right|\ge\left|x+1+2-x\right|=3\)
Đẳng thức xảy ra khi:
\(\left(x+1\right)\left(2-x\right)\ge0\)
\(\Leftrightarrow-1\le x\le2\)

\(b,B=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}-8}{x-5\sqrt{x}+6}\left(x\ge0;x\ne4;x\ne9\right)\\ B=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-4+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)
\(c,B< A\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}< \dfrac{\sqrt{x}+1}{\sqrt{x}-2}\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}< 0\\ \Leftrightarrow\dfrac{-5}{\sqrt{x}-2}< 0\Leftrightarrow\sqrt{x}-2>0\left(-5< 0\right)\\ \Leftrightarrow x>4\\ d,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=\dfrac{\sqrt{x}-4}{\sqrt{x}+1}=1-\dfrac{5}{\sqrt{x}+1}\in Z\\ \Leftrightarrow5⋮\sqrt{x}+1\Leftrightarrow\sqrt{x}+1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{-6;-2;0;4\right\}\\ \Leftrightarrow x\in\left\{0;16\right\}\left(\sqrt{x}\ge0\right)\)
\(e,P=1-\dfrac{5}{\sqrt{x}+1}\)
Ta có \(\sqrt{x}+1\ge1,\forall x\Leftrightarrow\dfrac{5}{\sqrt{x}+1}\ge5\Leftrightarrow1-\dfrac{5}{\sqrt{x}+1}\le-4\)
\(P_{max}=-4\Leftrightarrow x=0\)