Giúp e tìm tập xác định của các hs theo từng bước với ạ, do e ko giỏi phần này.E cảm ơn 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3.
\(y=\dfrac{1-sin^24x}{5}=\dfrac{cos^24x}{5}\)
\(cos4x\in\left[-1;1\right]\Rightarrow cos^24x\in\left[0;1\right]\Rightarrow y\in\left[0;\dfrac{1}{5}\right]\Rightarrow\left\{{}\begin{matrix}y_{min}=0\\y_{max}=\dfrac{1}{5}\end{matrix}\right.\)
6.
\(y=sinx+cosx+2=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\)
\(sin\left(x+\dfrac{\pi}{4}\right)\in\left[-1;1\right]\Rightarrow y=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\in\left[-\sqrt{2}+2;\sqrt{2}+2\right]\)
\(\Rightarrow y_{min}=-\sqrt{2}+2\)
\(y_{max}=\sqrt{2}+2\)

1, Hàm số xác định
⇔ cos2x ≠ 4
Mà 0 ≤ cos2x ≤ 1 nên điều trên đúng ∀ x ∈ R
Tập xác định : D = R
2, Hàm số xác định ⇔ \(\left\{{}\begin{matrix}cos3x\ne0\\cosx\ne0\end{matrix}\right.\)
⇔ cos3x ≠ 0
⇔ x ≠ \(\pm\dfrac{\pi}{6}+k.\dfrac{\pi}{3}\) , k ∈ Z
Tập xác định : D = R \ { \(\pm\dfrac{\pi}{6}+k.\dfrac{\pi}{3}\) , k ∈ Z}
3, D = [- 2 ; 2]
4, D = [- 1 ; +\(\infty\)) \ {0 ; 4}
11, sin2x - cos2x ≠ 0
⇔ cos2x ≠ 0


e: Ta có: \(2x\left(x-5\right)-26=x\left(2x+3\right)\)
\(\Leftrightarrow2x^2-10x-26-2x^2-3x=0\)
\(\Leftrightarrow-13x=26\)
hay x=-2
f: Ta có: \(x^2-9=-2x\left(x-3\right)\)
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)+2x\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(3x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
g: Ta có: \(4x^3-9x=0\)
\(\Leftrightarrow x\left(2x-3\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
h: Ta có: \(x^2-8x+2\left(x-8\right)=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
e. \(2x\left(x-5\right)-26=x\left(3+2x\right)\)
\(\Leftrightarrow2x^2-10x-26=3x+2x^2\)
\(\Leftrightarrow2x^2-10x-3x-2x^2=26\)
\(\Leftrightarrow-13x=26\) \(\Leftrightarrow x=-2\)
g. \(4x^3-9x=0\)
\(\Leftrightarrow x\left(4x^2-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\4x^2-9=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=\dfrac{9}{4}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm\dfrac{3}{2}\end{matrix}\right.\)
i. \(x^3-5x=0\)
\(\Leftrightarrow x\left(x^2-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-5=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=5\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm\sqrt{5}\end{matrix}\right.\)
k. \(x^2=10x-25\)
\(\Leftrightarrow x^2-10x+25=0\)
\(\Leftrightarrow\left(x-5\right)^2=0\)
\(\Leftrightarrow x-5=0\)
\(\Leftrightarrow x=5\)
f. \(x^2-9=-2x\left(x-3\right)\)
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)=-2x\left(x-3\right)\)
\(\Leftrightarrow x+3=-2x\)
\(\Leftrightarrow3x=-3\)
\(\Leftrightarrow x=-1\)
h. \(x^2-8x+2\left(x-8\right)=0\)
\(\Leftrightarrow x\left(x-8\right)+2\left(x-8\right)=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-8=0\\x+2=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
j. \(x\left(x-5\right)-x+5=0\)
\(\Leftrightarrow x\left(x-5\right)-\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\x-1=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\)
l. \(2x^3-72x=0\)
\(\Leftrightarrow2x\left(x^2-36\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-36=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=36\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm6\end{matrix}\right.\)

1.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=\left(-x^3-x\right)tan\left(-3x\right)=\left(x^3+x\right)tan3x=f\left(x\right)\)
Hàm chẵn
2.
\(D=R\)
\(f\left(-x\right)=\left(-2x+1\right)sin\left(-5x\right)=\left(2x-1\right)sin5x\ne\pm f\left(x\right)\)
Hàm không chẵn không lẻ
3.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=tan\left(-3x\right).sin\left(-5x\right)=-tan3x.\left(-sin5x\right)=tan3x.sin5x=f\left(x\right)\)
Hàm chẵn
4.
\(D=R\)
\(f\left(-x\right)=sin^2\left(-2x\right)+cos\left(-10x\right)=sin^22x+cos10x=f\left(x\right)\)
Hàm chẵn
5.
\(D=R\backslash\left\{k\pi\right\}\) là miền đối xứng
\(f\left(-x\right)=\dfrac{-x}{sin\left(-x\right)}=\dfrac{-x}{-sinx}=\dfrac{x}{sinx}=f\left(x\right)\)
Hàm chẵn


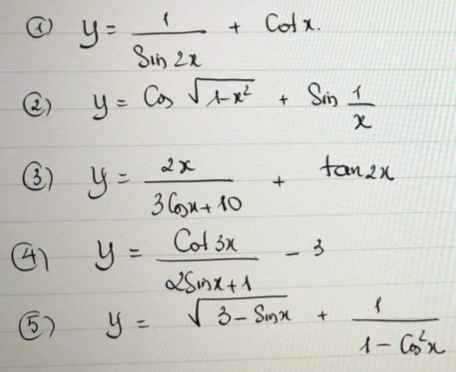
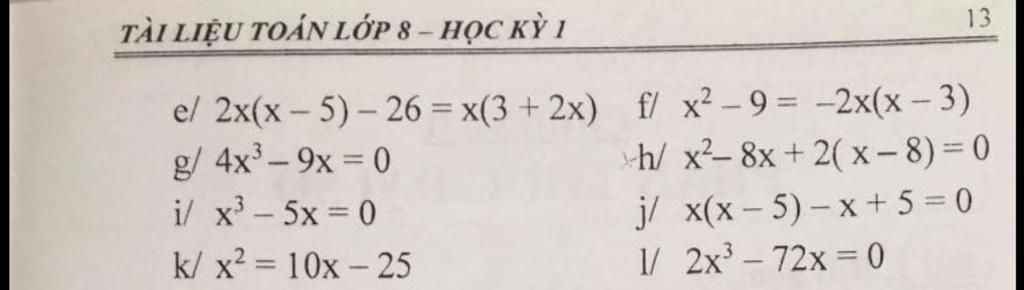
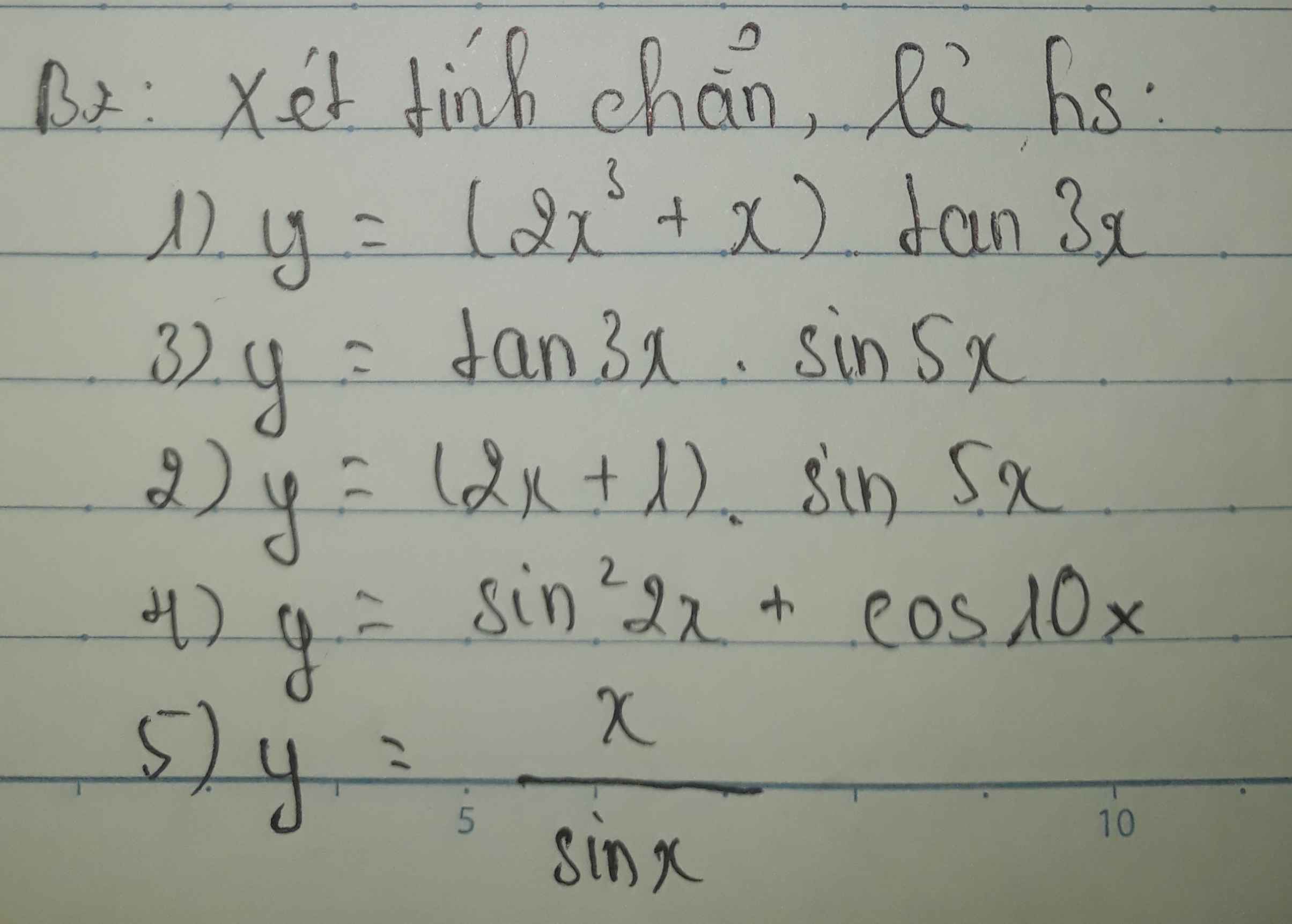
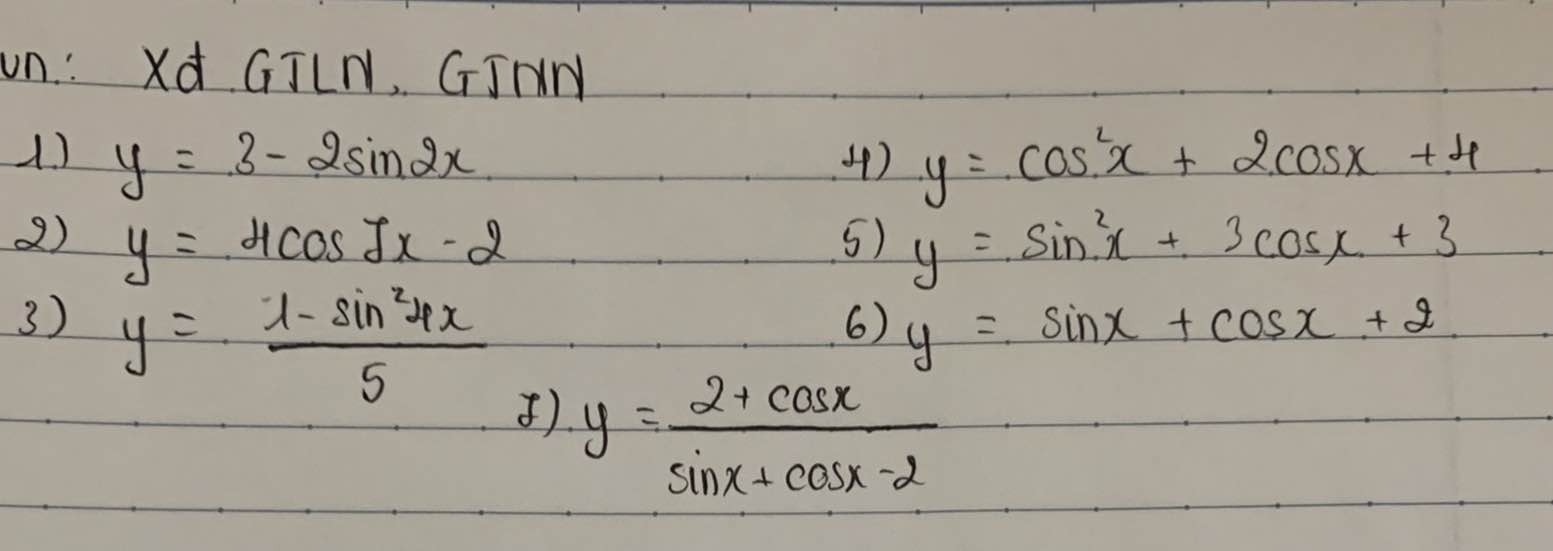
6.
Hàm số xác định khi \(\left\{{}\begin{matrix}2\sqrt{2}sinx-2\ne0\\sin3x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}sinx\ne\dfrac{1}{\sqrt{2}}\\sin3x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+k2\pi\\x\ne\dfrac{3\pi}{4}+k2\pi\\x\ne\dfrac{k\pi}{3}\end{matrix}\right.\).
10.
Hàm số xác định khi \(\left\{{}\begin{matrix}sin\left(3x+\dfrac{\pi}{6}\right)\ne0\\cos2x\ne0\\sinx+1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}sin\left(3x+\dfrac{\pi}{6}\right)\ne0\\cos2x\ne0\\sinx+1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-\dfrac{\pi}{18}+\dfrac{k\pi}{3}\\x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x\ne-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\).