làm sao để tìm được điểm rơi trong BĐT AM-GM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 7 2021
Cái này mình không sử dụng BĐT AM-GM
15 tháng 7 2021
\(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)
\(< =>\left(\dfrac{1}{a}+\dfrac{1}{b}\right).\left(a+b\right)\ge4\)
\(< =>1+\dfrac{b}{a}+\dfrac{a}{b}+1\ge4\)
\(< =>2+\dfrac{a}{b}+\dfrac{b}{a}\ge4\)(luôn đúng với mọi a,b là số thực dương)
Thật vậy có \(\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{a}{b}.\dfrac{b}{a}}=2\)(BĐT Cosi)
\(=>2+\dfrac{a}{b}+\dfrac{b}{a}\ge2+2=4\left(đpcm\right)\)
dấu"=" xảy ra<=>a=b
5 tháng 7 2021
\(\dfrac{\sqrt{a-4}}{a}+\dfrac{\sqrt{b-4}}{b}+\dfrac{\sqrt{c-4}}{c}=\dfrac{3}{4}\) (ĐK: \(a\ge4;b\ge4;c\ge4\))
Áp dụng AM-GM có:
\(2\sqrt{4\left(a-4\right)}\le4+a-4=a\)
\(\Rightarrow\dfrac{\sqrt{a-4}}{a}\le\dfrac{1}{4}\)
Tương tự cũng có: \(\dfrac{\sqrt{b-4}}{b}\le\dfrac{1}{4}\);\(\dfrac{\sqrt{c-4}}{c}\le\dfrac{1}{4}\)
Cộng vế với vế \(\Rightarrow VT\le\dfrac{3}{4}\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}4=a-4\\4=b-4\\4=c-4\end{matrix}\right.\)\(\Rightarrow a=b=c=8\) (tm)
Vậy...
29 tháng 6 2017
chứng minh nó thì phải cm am-gm 2 số sau đó là 4 số @@ dài lắm
DA
0
CB
1 tháng 6 2019
xD
Có: \(\frac{x^2-z^2}{y+z}+\frac{y^2-x^2}{z+x}+\frac{z^2-y^2}{x+y}\)(1)
\(=\frac{\left(x-z\right)\left(x+z\right)}{y+z}+\frac{\left(y-x\right)\left(x+y\right)}{z+x}+\frac{\left(z-y\right)\left(y+z\right)}{x+y}\)
\(\left(1\right)=S_1\left(x-z\right)^2+S_2\left(y-x\right)^2+S_3\left(z-y\right)^2\)
Trong đó:
\(\hept{\begin{cases}S_1=\frac{x+z}{\left(y+z\right)\left(x-z\right)}\\S_2=\frac{x+y}{\left(z+x\right)\left(y-x\right)}\\S_3=\frac{y+z}{\left(x+y\right)\left(z-y\right)}\end{cases}}\)
Giả sử: \(x\ge y\ge z\)( x,y,z lớn hơn 0)
Có: \(S_1=\frac{x+z}{\left(y+z\right)\left(x-z\right)}\ge0\)
Xét: \(S_1+S_2=\frac{x+z}{\left(y+z\right)\left(x-z\right)}-\frac{x+y}{\left(x+z\right)\left(x-y\right)}=\frac{\left(x+z\right)^2+\left(x+y\right)\left(y+z\right)^2+\left(y+z\right)\left(y-z\right)\left(2x+y+z\right)}{.....}\ge0\)
Xét tiếp \(S_1+S_3\)là xong
Không biết đúng k tại mình hơi yếu
T
1 tháng 6 2019
*Nếu được giả sử như bạn Cà Bùi thì bài làm của em như sau,mong mọi người góp ý ạ!
Ta có: \(VT=\frac{x^2-z^2}{y+z}+\frac{y^2-x^2}{z+x}-\frac{x^2-z^2+y^2-x^2}{x+y}\)
\(=\left(x^2-z^2\right)\left(\frac{x+y-y-z}{\left(x+y\right)\left(y+z\right)}\right)+\left(y^2-x^2\right)\left(\frac{x+y-z-x}{\left(z+x\right)\left(x+y\right)}\right)\) (nhóm các số thích hợp + quy đồng)
\(=\frac{\left(x+z\right)\left(x-z\right)^2}{\left(x+y\right)\left(y+z\right)}+\frac{\left(y-x\right)\left(y-z\right)}{\left(z+x\right)}\)
Do a, b, c có tính chất hoán vị, nên ta giả sử y là số lớn nhất. Khi đó vế trái không âm hay ta có đpcm.
AH
Akai Haruma
Giáo viên
7 tháng 10 2021
Bạn lên google gõ các chuyên đề về BĐT Bunhiacopxky có rất nhiều mà.
$(a_1^2+a_2^2+...+a_n^2)(b_1^2+b_2^2+...+b_n^2)\geq (a_1b_1+a_2b_2+...+a_nb_n)^2$
Dấu "=" xảy ra khi:
$\frac{a_1}{b_1}=\frac{a_2}{b_2}=...=\frac{a_n}{b_n}$
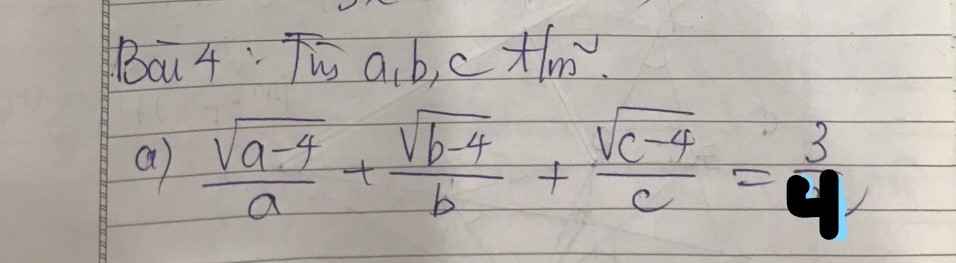
tra google