Tìm các số tự nhiên x, y thỏa mãn : x2 + 3y2 + 4xy + 4x + 10y - 12 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
7
PT
1
5 tháng 3 2021
16x2 - 2xy2 - 3y2 + 24x = -336
\(\Leftrightarrow\) 16x2 - 2xy2 - 3y2 + 24x = -336
\(\Leftrightarrow\) 2x(8x - y2) + 3(8x - y2) = -336
\(\Leftrightarrow\) (8x - y2)(2x + 3) = -336
Đến đây chắc tự tìm được r
Chúc bn học tốt!
2V
1
NV
2 tháng 3 2023
\(x^2y^2-x^2-3y^2-2x-1=0\)
\(\Leftrightarrow y^2\left(x^2-3\right)-\left(x+1\right)^2=0\)
\(\Leftrightarrow y^2\left(x^2-3\right)=\left(x+1\right)^2\left(1\right)\)
Vì y2 và (x+1)2 đều là các số chính phương, do đó x2-3 cũng phải là số chính phương.
Đặt \(x^2-3=a^2\) (a là số tự nhiên).
\(\Leftrightarrow\left(x-a\right)\left(x+a\right)=3\)
Ta có x+a>x-a. Lập bảng:
| x+a | 3 | -1 |
| x-a | 1 | -3 |
| x | 2 | -2 |
Với \(x=2\) . \(\left(1\right)\Rightarrow y^2=9\Leftrightarrow y=\pm3\)
Với \(x=-2\). \(\left(1\right)\Rightarrow y^2=1\Leftrightarrow y=\pm1\)
Vậy các số nguyên \(\left(x;y\right)=\left(2;3\right),\left(2;-3\right),\left(-2;1\right),\left(-2;-1\right)\)
13 tháng 1 2023
3x^2+3y^2+4xy-2x+2y+2=0
=>2x^2+4xy+2y^2+x^2-2x+1+y^2+2y+1=0
=>x=1 và y=-1
M=(1-1)^2017+(1-2)^2018+(-1+1)^2015=1
TT
1
13 tháng 1 2018
pt <=> 9x^2+3y^2+12xy+12x+6y+15 = 0
<=> [(9x^2+12xy+4y^2)+2.(3x+2y).2+4] - (y^2+2y+1) + 12 = 0
<=> [(3x+2y)^2+2.(3x+2y).2+4] -(y+1)^2 = -12
<=> (3x+2y+2)^2 - (y+1)^2 = -12
<=> (3x+2y+2+y+1).(3x+2y+2-y-1) = -12
<=> (3x+3y+3).(3x+y+1) = -12
<=> (x+y+1).(3x+y+1) = -4
Đến đó bạn dùng quan hệ ước bội cho các số nguyên mà giải nha !
Tk mk nha
KJ
1
18 tháng 8 2019
\(4x^2+4y-4xy+5y^2+1=0\)
\(\Leftrightarrow\left(2x-y\right)^2+\left(2y+1\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}x=-\frac{1}{4}\\y=-\frac{1}{2}\end{cases}}\)
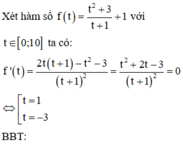
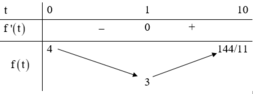
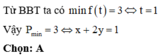
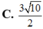
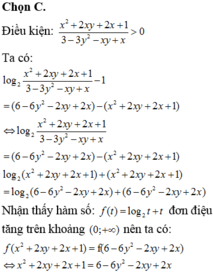
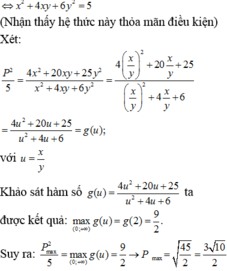
\(x^2+3y^2+4xy+4x+10y-12=0\)
\(\Leftrightarrow\left(x^2+4y^2+4+4xy+4x+8y\right)-\left(y^2-2y+1\right)-17=0\)
\(\Leftrightarrow\left(x+2y+2\right)^2-\left(y-1\right)^2=17\)
\(\Leftrightarrow\left(x+3y+1\right)\left(x+y+3\right)=17\)
. . . . . . . . . . . . .. . . . . . . . . . . . .
M giỏi ghê á :v