Cho hàm số y = 2x + 1 và y = 3x − 1 có đồ thị là d1 và d2. Vẽ d1, d2 trên cùng một hệ
trục tọa độ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NV
1
Những câu hỏi liên quan
3 tháng 1 2022
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x-5=\dfrac{1}{2}x\\y=2x-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{2}x=5\\y=2x-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{10}{3}\\y=2\cdot\dfrac{10}{3}-5=\dfrac{20}{3}-\dfrac{15}{3}=\dfrac{5}{3}\end{matrix}\right.\)
CM
18 tháng 9 2019
a) Tập xác định của hàm số R
Bảng giá trị
| x | 0 | 1 |
| y = -2x + 3 | 3 | 1 |
| x | 0 | 1 |
| y = x – 1 | - 1 | 0 |
31 tháng 10 2021
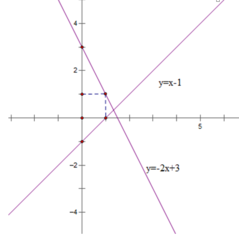
b, PT hoành độ giao điểm là \(2x-1=-x+5\Leftrightarrow3x=6\Leftrightarrow x=2\Leftrightarrow y=3\)
\(\Leftrightarrow A\left(2;3\right)\)
Vậy A(2;3) là tọa độ giao điểm 2 đths
5 tháng 10 2021
a, tự vẽ
b, Hoành độ giao điểm thỏa mãn phương trình
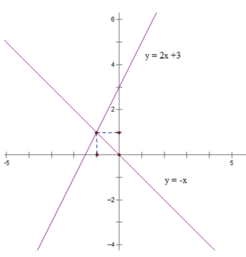
\(2x+3=-x\Leftrightarrow3x=-3\Leftrightarrow x=-1\Rightarrow y=1\)
Vậy \(x=-1;y=1\)
CM
6 tháng 6 2019
a) Tập xác định R
Bảng giá trị:
| x | 0 | -1 |
| y = 2x + 3 | 3 | 1 |
| x | 0 | -1 |
| y = - x | 0 | 1 |
ND
0
=)))))