Xác định lực hút giữa TĐ và Mặt Trăng nếu khối lượng tương ứng của chúng là: M1=6x1024kg; M2= 7,2x1022kg và khoảng cách giữa hai tâm của chúng là: 3,8x105 km. Tại điểm nào trên đường nối tâm của chúng, lực hấp dẫn đặt vào một vật tại đó triệt tiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
Lực mà trái đất hút mặt trăng là:
F = G . M . m r 2 = 6 , 67.10 − 11 .6.10 24 .7 , 37.10 22 38.10 7 2 = 2 , 04.10 20 N

Chọn đáp án D
Lực hấp dẫn do mặt trăng tác dụng lên vật là:
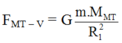
Lực hấp dẫn do trái đất tác dụng lên vật là:
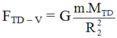
FMT – V = FTD – V
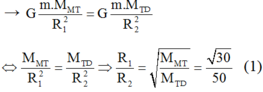
Lại có:
R1 + R2 = 3,84.108 (2)
Từ (1), (2)
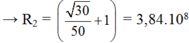
→ R2 = 3,46.108m.

\(F_{hapdan}=G\dfrac{m'm''}{r^2}=6,67\cdot10^{-11}\dfrac{6\cdot10^{24}\cdot7,2\cdot10^{22}}{\left(3,8\cdot10^5\cdot1000\right)^2}=.......\left(N\right)\)
\(F=G\cdot\dfrac{M_1M_2}{d^2}=6,67\cdot10^{-11}\cdot\dfrac{6\cdot10^{24}\cdot7,2\cdot10^{22}}{\left(3,8\cdot10^5\cdot10^3\right)^2}=2\cdot10^{20}\)(N)
Chọn C

Lực hấp dẫn:
\(F_{hd}=G\cdot\dfrac{m_1\cdot m_2}{R^2}=16\)
Nếu tăng khoảng cách lên gấp đôi thì lực hút tức lực tương tác lúc này là:
\(F_{hd}'=G\cdot\dfrac{m_1\cdot m_2}{R'^2}=G\cdot\dfrac{m_1\cdot m_2}{\left(2R\right)^2}=\dfrac{1}{4}\cdot G\cdot\dfrac{m_1\cdot m_2}{R^2}=\dfrac{1}{4}F_{hd}\)
Vậy lực hấp dẫn mới giảm 4 lần và
\(F_{hd}'=\dfrac{1}{4}F_{hd}=\dfrac{1}{4}\cdot16=4N\)

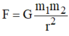
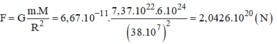

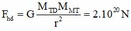
khoảng cách đường nối tâm R
khoảng cách từ vật đến trái đất là x
khoảng cách từ vật đến mặt trăng là R-x
lực hấp dẫn vào vật của trái đất và mặt trăng triệt tiêu
\(F_{hd1}=F_{hd2}\Leftrightarrow\dfrac{G.m.M_1}{x^2}=\dfrac{G.m.M_2}{\left(R-x\right)^2}\)
\(\Rightarrow x\approx\).............