chứng minh rằng: \(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\)với mọi số x,y nguyên dương
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x^3}{y+2z}+\dfrac{y^3}{z+2x}+\dfrac{z^3}{x+2y}=\dfrac{x^4}{xy+2xz}+\dfrac{y^4}{yz+2xy}+\dfrac{z^4}{xz+2yz}\)
\(\ge\dfrac{\left(x^2+y^2+z^2\right)^2}{3\left(xy+yz+zx\right)}\ge\dfrac{\left(x^2+y^2+z^2\right)^2}{3\left(x^2+y^2+z^2\right)}=\dfrac{1}{3}\)
Dấu "=" xảy ra khi \(x=y=z=\dfrac{1}{\sqrt{3}}\)

\(\left(x+y+z\right)^2=x^2+y^2+z^2+2xy+2xz+2yz=z^2+\left(x+y\right)^2+2z\left(x+y\right)=36\)
áp dụng BĐT cosi :
\(z^2+\left(x+y\right)^2\ge2z\left(x+y\right)\)
<=> \(z^2+\left(x+y\right)^2+2z\left(x+y\right)\ge4z\left(x+y\right)=36< =>z\left(x+y\right)\ge9\)
ta lại có \(\dfrac{x+y}{xyz}=\dfrac{x}{xyz}+\dfrac{y}{xyz}=\dfrac{1}{yz}+\dfrac{1}{xz}\) áp dụng BĐT buhihacopxki dạng phân thức => \(\dfrac{1}{yz}+\dfrac{1}{xz}\ge\dfrac{4}{yz+xz}=\dfrac{4}{z\left(x+y\right)}\ge\dfrac{4}{9}\left(đpcm\right)\)
dấu bằng xảy ra khi \(\left[{}\begin{matrix}yz=xz< =>x=y\\x+y+z=6\\z^2=\left(x+y\right)^2\end{matrix}\right.< =>\left[{}\begin{matrix}x+y+z=6\\z=2x=2y\end{matrix}\right.< =>\left[{}\begin{matrix}x=y=\dfrac{3}{2}\\z=3\end{matrix}\right.\)
-Ủa vì sao\(\dfrac{4}{z\left(x+y\right)}\ge\dfrac{4}{9}\)? Đáng lẽ là \(\dfrac{4}{z\left(x+y\right)}\le\dfrac{4}{9}\) chứ?

Áp dụng BĐT cosi cho 3 số x;y;z dương
\(\dfrac{x^2}{y^2}+\dfrac{y^2}{z^2}\ge2\sqrt{\dfrac{x^2y^2}{y^2z^2}}=\dfrac{2x}{z}\\ \dfrac{y^2}{z^2}+\dfrac{z^2}{x^2}\ge2\sqrt{\dfrac{y^2z^2}{x^2z^2}}=\dfrac{2y}{z}\\ \dfrac{x^2}{y^2}+\dfrac{z^2}{x^2}\ge2\sqrt{\dfrac{x^2z^2}{x^2y^2}}=\dfrac{2z}{y}\)
Cộng vế theo vế
\(\Leftrightarrow2\left(\dfrac{x^2}{y^2}+\dfrac{y^2}{z^2}+\dfrac{x^2}{z^2}\right)\ge2\left(\dfrac{x}{y}+\dfrac{y}{z}+\dfrac{z}{x}\right)\)
\(\LeftrightarrowĐpcm\)
Cám ơn thầy ạ, tuy nhiên hình như là có sự nhầm lẫn rồi thầy ạ, bài này thầy xem lại đề bài giúp em với ạ

Có \(VT=\dfrac{x^2}{x^3-xyz+2013x}+\dfrac{y^2}{y^3-xyz+2013y}+\dfrac{z^2}{z^3-xyz+2013z}\)
\(\ge\dfrac{\left(x+y+z\right)^2}{x^3+y^3+z^3-3xyz+2013\left(x+y+z\right)}\)
\(=\dfrac{\left(x+y+z\right)^2}{\left(x+y+z\right)\left[x^2+y^2+z^2-\left(xy+yz+zx\right)\right]+2013\left(x+y+z\right)}\)
\(=\dfrac{x+y+z}{x^2+y^2+z^2-\left(xy+yz+zx\right)+3\left(xy+yz+zx\right)}\)
(vì \(2013=3.671=3\left(xy+yz+zx\right)\))
\(=\dfrac{x+y+z}{x^2+y^2+z^2+2\left(xy+yz+zx\right)}\)
\(=\dfrac{x+y+z}{\left(x+y+z\right)^2}\)
\(=\dfrac{1}{x+y+z}\)
ĐTXR \(\Leftrightarrow\dfrac{1}{x^2-yz+2013}=\dfrac{1}{y^2-zx+2013}=\dfrac{1}{z^2-xy+2013}\)
\(\Leftrightarrow x^2-yz=y^2-zx=z^2-xy\)
\(\Leftrightarrow x=y=z\) (với \(x,y,z>0\))
Vậy ta có đpcm.

a: Thiếu vế phải rồi bạn
b: \(\Leftrightarrow\dfrac{x+y}{xy}>=\dfrac{4}{x+y}\)
\(\Leftrightarrow\left(x+y\right)^2>=4xy\)
\(\Leftrightarrow\left(x-y\right)^2>=0\)(luôn đúng)

\(\dfrac{x^2}{y^2}+\dfrac{y^2}{z^2}\ge\dfrac{2x}{z}\); \(\dfrac{y^2}{z^2}+\dfrac{z^2}{x^2}\ge\dfrac{2y}{x}\); \(\dfrac{x^2}{y^2}+\dfrac{z^2}{x^2}\ge\dfrac{2z}{y}\)
Cộng ba vế bđt sau đó chia 2 ta được đpcm
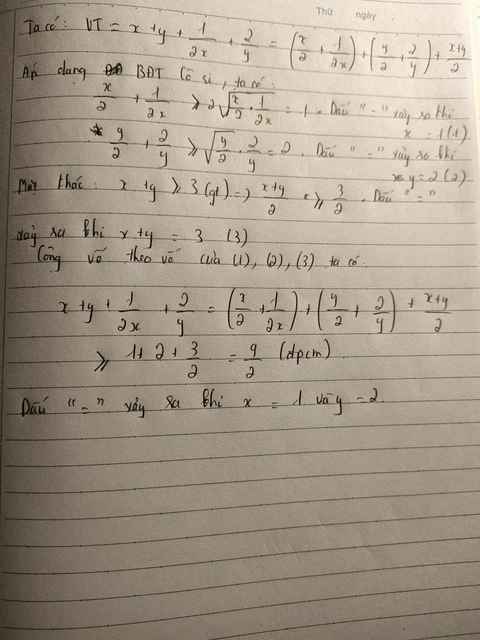


C1:Biến đổi tương đương
\(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\Leftrightarrow\dfrac{x}{xy}+\dfrac{y}{xy}\ge\dfrac{4}{x+y}\)
\(\Leftrightarrow\dfrac{x+y}{xy}\ge\dfrac{4}{x+y}\Leftrightarrow\left(x+y\right)^2\ge4xy\)
\(\Leftrightarrow x^2+y^2+2xy\ge4xy\Leftrightarrow x^2+y^2-2xy\ge0\Leftrightarrow\left(x-y\right)^2\ge0\)
C2:Dùng AM-GM
\(x+y\ge2\sqrt{xy}\);\(\dfrac{1}{x}+\dfrac{1}{y}\ge2\sqrt{\dfrac{1}{x}\cdot\dfrac{1}{y}}=2\sqrt{\dfrac{1}{xy}}\)
Nhân theo vế 2 BĐT
\(\left(x+y\right)\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\ge4\sqrt{xy\cdot\dfrac{1}{xy}}=4\Rightarrow\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\)
C3:Dùng Cauchy-Schwarz (dạng Engel)
\(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{\left(1+1\right)^2}{x+y}=\dfrac{4}{x+y}\)
-3 cách trên đều có dấu "=" khi \(x=y\)