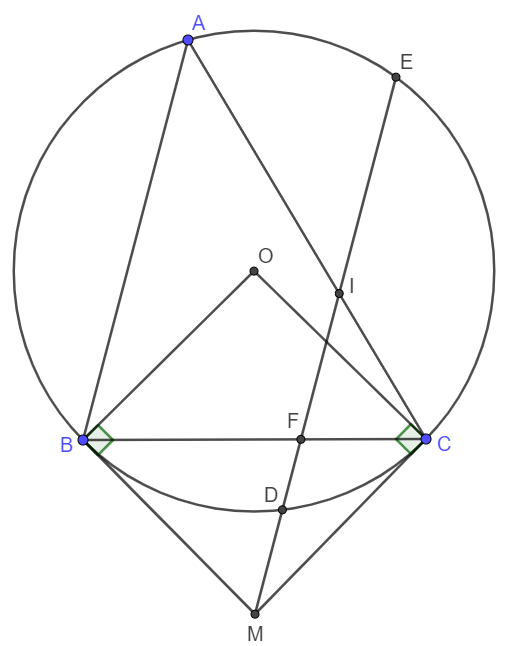
Cho tam giác nhọn ABC nội tiếp (O) . Tiếp tuyến tại B và C của đường tròn cắt nhau tại D. Từ D kẻ đường thẳng song song vs AB, đường thẳng này cắt đường tròn tại E và F, cắt AC tại I ( E nằm trên cung nhỏ BC)
a, CM tứ giác BDCO nt được
b, CM: DC\(^2\)=DE.DF
c, chứng tỏ I là trung điểm của EF

HÌNH BẠN TỰ VẼ NHA
a )
Xét tứ giác BDCO , co :
\(\widehat{B}=90^o\left(gt\right)\)
\(\widehat{C}=90^o\left(gt\right)\)
\(\widehat{B}+\widehat{C}=90^o+90^o=180^o\)
Vay : tứ giác BDCO nội tiếp ( vì có tổng số đo hai góc đối diện bằng 180o )
b ) Xét \(\Delta DCEva\Delta DFC,co:\)
\(\widehat{D}\) là góc chung
\(\widehat{ECD}=\widehat{EFC}\) ( góc tạo bởi tia tiếp tuyến và dây cung bằng góc nội tiếp cùng chắn 1 cung )
Do do : \(\Delta DCE~\Delta DFC\left(g-g\right)\)
=> \(\frac{DC}{DE}=\frac{DF}{DC}\)
=> DC2 = DE . DF
ta có góc DIC=AIF ( đđ )
mà góc AIF = IAB (slt)
gọi H là giao điểm của OD với đường tròn
mà góc IAB = COD ( =1/2 cung CB )( Vì ACB là góc nội tiếp chắn cung CB và COD là góc ở tâm chắn cung CH mà Cung CH= cung BH= cung CB/2)
từ đó suy ra góc CID= COD
suy ra tứ giác CIOD nội tiếp( hai góc bằng nhau cùng chắn cung CD)
suy ra góc OID=OCD=90°
suy ra OI vuông với EF
suy ra I là trung điểm của EF(đpcm)