Giúp em bài giải phương trình với bài hệ với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
mọi ng giải hộ em bài này với ạ( có lập bảng và giải bằng hệ phương trình ạ) e cần gấp
0
2 tháng 2 2023
Gọi tuổi của em và chị lần lượt là a,b
Theo đề, ta có: \(\left\{{}\begin{matrix}a-8+b-8=24\\a=\dfrac{3}{5}b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=40\\a-\dfrac{3}{5}b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=15\\b=25\end{matrix}\right.\)
MA
ĐỀ BÀI: GIẢI HỆ PHƯƠNG TRÌNH. Gíup em với ạ. Em cảm ơn!
0
KH
3
KV
23 tháng 4 2021
\(\dfrac{x+2}{x-1}=\dfrac{x-1}{x-3}\) (1)
ĐKXĐ: \(x\ne1;x\ne3\)
(1) \(\Leftrightarrow\left(x+2\right)\left(x-3\right)=\left(x-1\right)^2\)
\(\Leftrightarrow x^2-3x+2x-6=x^2-2x+1\)
\(\Leftrightarrow-3x+2x+2x=1+6\)
\(\Leftrightarrow x=7\) (nhận)
Vậy S = {7}
PP
1
8 tháng 12 2021
\(ĐK:x\ne\dfrac{1}{2};x\ne1;x\ne\dfrac{3}{2};x\ne2;x\ne\dfrac{5}{2}\\ PT\Leftrightarrow\dfrac{1}{\left(2x-1\right)\left(x-1\right)}+\dfrac{1}{\left(x-1\right)\left(3x-2\right)}+\dfrac{1}{\left(3x-2\right)\left(x-2\right)}+\dfrac{1}{\left(x-2\right)\left(5x-2\right)}=\dfrac{4}{21}\\ \Leftrightarrow2\left[\dfrac{\dfrac{1}{2}}{\left(x-\dfrac{1}{2}\right)\left(x-1\right)}+\dfrac{\dfrac{1}{2}}{\left(x-1\right)\left(x-\dfrac{3}{2}\right)}+\dfrac{\dfrac{1}{2}}{\left(x-\dfrac{3}{2}\right)\left(x-2\right)}+\dfrac{\dfrac{1}{2}}{\left(x-2\right)\left(x-\dfrac{5}{2}\right)}\right]=\dfrac{4}{21}\)
\(\Leftrightarrow\dfrac{1}{x-1}-\dfrac{1}{x-\dfrac{1}{2}}+\dfrac{1}{x-\dfrac{3}{2}}-\dfrac{1}{x-1}+\dfrac{1}{x-2}-\dfrac{1}{x-\dfrac{3}{2}}+\dfrac{1}{x-\dfrac{5}{2}}-\dfrac{1}{x-2}=\dfrac{2}{21}\\ \Leftrightarrow\dfrac{1}{x-1}-\dfrac{1}{x-\dfrac{5}{2}}=\dfrac{2}{21}\\ \Leftrightarrow\dfrac{x-\dfrac{5}{2}-x+1}{\left(x-1\right)\left(x-\dfrac{5}{2}\right)}=\dfrac{2}{21}\\ \Leftrightarrow\dfrac{-\dfrac{3}{2}}{x^2-\dfrac{7}{2}x+\dfrac{5}{2}}=\dfrac{2}{21}\\ \Leftrightarrow x^2-\dfrac{7}{2}x+\dfrac{5}{2}=-\dfrac{63}{4}\\ \Leftrightarrow4x^2-14x+10=-63\\ \Leftrightarrow4x^2-14x+73=0\\ \Leftrightarrow x\in\varnothing\)
TH
0
CH
Cô Hoàng Huyền
Admin
VIP
30 tháng 5 2016
Cô làm câu b thôi nhé :)
Ta có hệ \(\hept{\begin{cases}mx+4y=10-m\\x+my=4\end{cases}}\Leftrightarrow\hept{\begin{cases}m\left(4-my\right)+4y=10-m\\x=4-my\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(4-m^2\right)y=10-5m\left(1\right)\\x=4-my\end{cases}}\)
Với \(4-m^2=0\Leftrightarrow m=2\) hoặc \(m=-2\)
Xét m =2, phương trình (1) tương đương 0.x = 0. Vậy hệ phương trình có vô số nghiệm dạng \(\left(4-2t;t\right)\)
Xét m = -2, phương trình (1) tương đương 0.x = 20. Vậy hệ phương trình vô nghiệm.
Với \(4-m^2\ne0\Leftrightarrow m\ne2\) và \(m\ne-2\), phương trình (1) tương đương \(y=\frac{10-5m}{4-m^2}=\frac{5}{2+m}\)
Từ đó : \(x=\frac{8-m}{2+m}\)
Kết luận:
+ m = 2, hệ phương trình có vô số nghiệm dạng \(\left(4-2t;t\right)\)
+ m = - 2, hệ phương trình vô nghiệm.
+ \(m\ne2;m\ne-2\) hệ có 1 nghiệm duy nhất \(\hept{\begin{cases}x=\frac{8-m}{2+m}\\y=\frac{5}{2+m}\end{cases}}\)
Chúc em học tập tốt :)
NT
2
11 tháng 4 2022
\(\left\{{}\begin{matrix}4x+5y=9\\2x-y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4x+5y=9\\10x-5y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}14x=14\\4x+5y=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\4.1+5y=9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
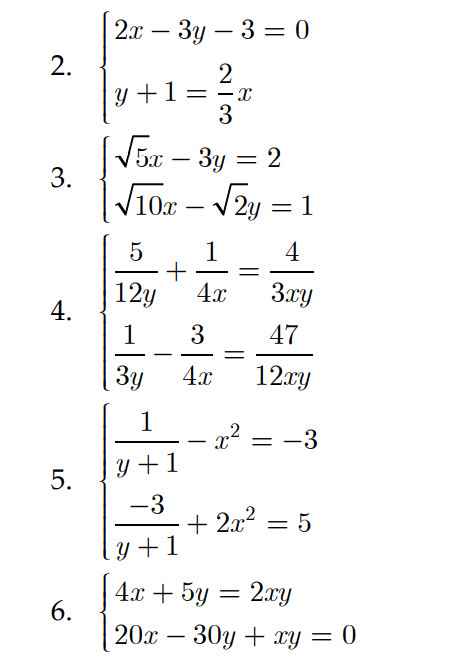
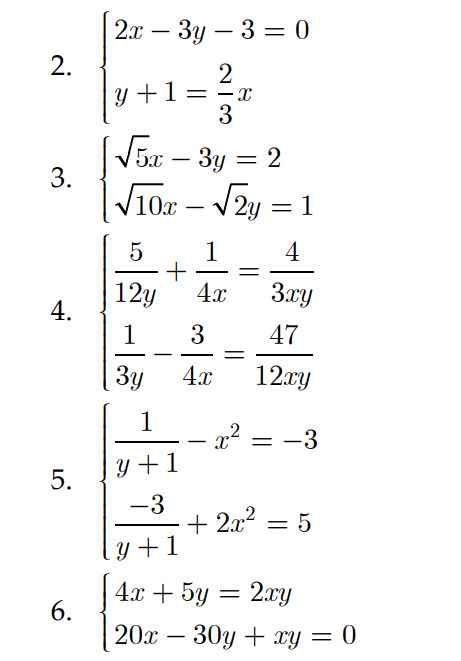
a) đk \(x\ge\dfrac{-3}{2}\)
PT <=> \(4x^2\left(2x+3\right)=\left(3x^2+6x+1\right)^2\)
<=> \(8x^3+12x^2=9x^4+36x^2+1+36x^3+12x+6x^2\)
<=> \(9x^4+28x^3+30x^2+12x+1=0\)
<=> \(\left(x+1\right)^3\left(9x+1\right)=0\)
<=> \(\left[{}\begin{matrix}x=-1\left(c\right)\\x=\dfrac{-1}{9}\left(l\right)\end{matrix}\right.\)
KL: PT có nghiệm duy nhất x = -1
b) đk: \(x\ge-1;x\ge2y\)
hpt <=> \(\left\{{}\begin{matrix}2x^2-4xy+3y-4x-4=\sqrt{9\left(x-1\right)\left(x+1\right)\left(x-2y\right)}\left(1\right)\\2x-2y+1+2\sqrt{\left(x+1\right)\left(x-2y\right)}=2x-2y+5\left(2\right)\end{matrix}\right.\)
(2) <=> \(\sqrt{\left(x+1\right)\left(x-2y\right)}=2\)
<=> \(\left(x+1\right)\left(x-2y\right)=4\)
(1) <=> 2(x+1)(x-2y) + x - 4 = \(6.\sqrt{x-1}\)
<=> x+4 = \(6\sqrt{x-1}\)
<=> x2 + 8x + 16 = 36x - 36
<=> x2 -28x + 52 = 0
<=> (x-26)(x-2) = 0
<=> \(\left[{}\begin{matrix}x=26< =>y=\dfrac{349}{27}\\x=2< =>y=\dfrac{1}{3}\end{matrix}\right.\)