Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Rightarrow\dfrac{1}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{1}{\left(2x-2\right)\left(2x-3\right)}+\dfrac{1}{\left(2x-3\right)\left(2x-4\right)}+\dfrac{1}{\left(2x-4\right)\left(2x-5\right)}=\dfrac{4}{21}\)
\(\Rightarrow\dfrac{1}{2x-2}-\dfrac{1}{2x-1}+\dfrac{1}{2x-3}-\dfrac{1}{2x-2}+\dfrac{1}{2x-4}-\dfrac{1}{2x-3}+\dfrac{1}{2x-5}-\dfrac{1}{2x-4}=\dfrac{4}{21}\)
\(\Rightarrow\dfrac{1}{2x-5}-\dfrac{1}{2x-1}=\dfrac{4}{21}\)
\(\Rightarrow\dfrac{4}{\left(2x-1\right)\left(2x-5\right)}=\dfrac{4}{21}\)
\(\Rightarrow\left(2x-1\right)\left(2x-5\right)=21\)
\(\Rightarrow4x^2-12x-16=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=4\end{matrix}\right.\)

\(\dfrac{x+2}{x-1}=\dfrac{x-1}{x-3}\) (1)
ĐKXĐ: \(x\ne1;x\ne3\)
(1) \(\Leftrightarrow\left(x+2\right)\left(x-3\right)=\left(x-1\right)^2\)
\(\Leftrightarrow x^2-3x+2x-6=x^2-2x+1\)
\(\Leftrightarrow-3x+2x+2x=1+6\)
\(\Leftrightarrow x=7\) (nhận)
Vậy S = {7}

\(x^2\left(x+4,5\right)=13,5\)
<=>\(x^3+4,5x^2-13,5=0\)
<=> \(x^3+3x^2+1,5x^2+4,5x-4,5x-13,5=0\)
<=>\(x^2\left(x+3\right)+1,5x\left(x+3\right)-4,5\left(x+3\right)=0\)
<=>\(\left(x+3\right)\left(x^2+1,5x-4,5\right)=0\)
<=>\(\left(x+3\right)\left[x^2+3x-1,5-4,5\right]=0\)
<=>\(\left(x+3\right)\left[x\left(x+3\right)-1,5\left(x+3\right)\right]=0\)
<=>\(\left(x+3\right)^2\left(x-1,5\right)=0\)
<=> \(\left[{}\begin{matrix}\left(x+3\right)^2=0\\x-1,5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1,5\end{matrix}\right.\)
Vậy...
Ta có: \(x^2\left(x+4.5\right)=13.5\)
\(\Leftrightarrow x^3+\dfrac{9}{2}x^2-\dfrac{27}{2}=0\)
\(\Leftrightarrow2x^3+9x^2-27=0\)
\(\Leftrightarrow2x^3-3x^2+12x^2-18x+18x-27=0\)
\(\Leftrightarrow x^2\left(2x-3\right)+12x\left(2x-3\right)+9\left(2x-3\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(x^2+12x+9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\x^2+12x+9=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\\left(x+6\right)^2=27\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x+6=3\sqrt{3}\\x+6=-3\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=3\sqrt{3}-6\\x=-3\sqrt{3}-6\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{3}{2};3\sqrt{3}-6;-3\sqrt{3}-6\right\}\)

Bài 8:
a: Khi a=1 thì phương trình sẽ là \(\left(1-4\right)x-12x+7=0\)
=>-3x-12x+7=0
=>-15x+7=0
=>-15x=-7
hay x=7/15
b: Thay x=1 vào pt, ta được:
\(a^2-4-12+7=0\)
\(\Leftrightarrow\left(a-3\right)\left(a+3\right)=0\)
hay \(a\in\left\{3;-3\right\}\)
c: Pt suy ra là \(\left(a^2-16\right)x+7=0\)
Để phương trình đã cho luôn có một nghiệm duy nhất thì (a-4)(a+4)<>0
hay \(a\notin\left\{4;-4\right\}\)

=>0,2x+0,4-0,5x=0,25-0,5x+0,25
=>0,2x+0,4=0,5
=>0,2x=0,1
=>x=1/2

4x2y3=2x2.2y2.y
6x3y2=2.3.x2y2.x
=> MTC= 2.2.3.x3y3=12x3y3
4x2y3=2x2.2y2.y
6x3y2=2.3.x2y2.x
=> MTC= 2.2.3.x3y3=12x3y3

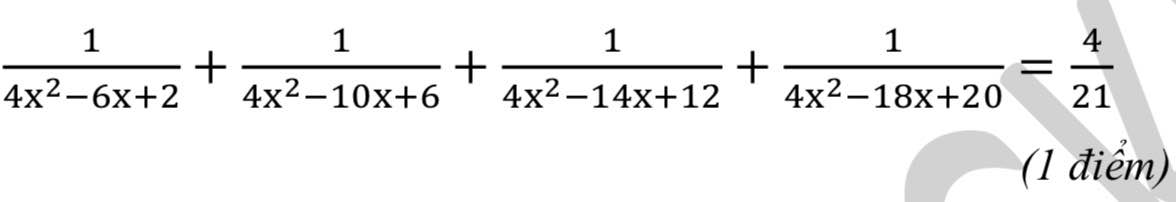


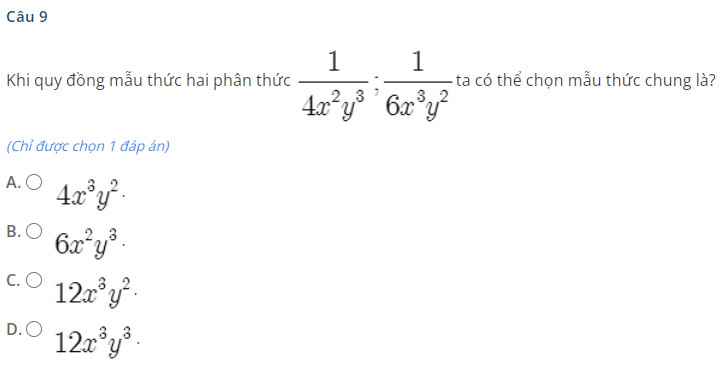






\(ĐK:x\ne\dfrac{1}{2};x\ne1;x\ne\dfrac{3}{2};x\ne2;x\ne\dfrac{5}{2}\\ PT\Leftrightarrow\dfrac{1}{\left(2x-1\right)\left(x-1\right)}+\dfrac{1}{\left(x-1\right)\left(3x-2\right)}+\dfrac{1}{\left(3x-2\right)\left(x-2\right)}+\dfrac{1}{\left(x-2\right)\left(5x-2\right)}=\dfrac{4}{21}\\ \Leftrightarrow2\left[\dfrac{\dfrac{1}{2}}{\left(x-\dfrac{1}{2}\right)\left(x-1\right)}+\dfrac{\dfrac{1}{2}}{\left(x-1\right)\left(x-\dfrac{3}{2}\right)}+\dfrac{\dfrac{1}{2}}{\left(x-\dfrac{3}{2}\right)\left(x-2\right)}+\dfrac{\dfrac{1}{2}}{\left(x-2\right)\left(x-\dfrac{5}{2}\right)}\right]=\dfrac{4}{21}\)
\(\Leftrightarrow\dfrac{1}{x-1}-\dfrac{1}{x-\dfrac{1}{2}}+\dfrac{1}{x-\dfrac{3}{2}}-\dfrac{1}{x-1}+\dfrac{1}{x-2}-\dfrac{1}{x-\dfrac{3}{2}}+\dfrac{1}{x-\dfrac{5}{2}}-\dfrac{1}{x-2}=\dfrac{2}{21}\\ \Leftrightarrow\dfrac{1}{x-1}-\dfrac{1}{x-\dfrac{5}{2}}=\dfrac{2}{21}\\ \Leftrightarrow\dfrac{x-\dfrac{5}{2}-x+1}{\left(x-1\right)\left(x-\dfrac{5}{2}\right)}=\dfrac{2}{21}\\ \Leftrightarrow\dfrac{-\dfrac{3}{2}}{x^2-\dfrac{7}{2}x+\dfrac{5}{2}}=\dfrac{2}{21}\\ \Leftrightarrow x^2-\dfrac{7}{2}x+\dfrac{5}{2}=-\dfrac{63}{4}\\ \Leftrightarrow4x^2-14x+10=-63\\ \Leftrightarrow4x^2-14x+73=0\\ \Leftrightarrow x\in\varnothing\)