Cho tam giác ABC vuông tại A có đường phân giác BK. Kẻ KI vuông góc với BC
a) Chứng minh rằng tam giác ABK=tam giác IBK.
b)Kẻ đường cao AH của tam giác ABC. Chứng minh rằng AI là tia phân giác của góc HAC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 5 2021
b) Ta có: KI\(\perp\)BC(gt)
AH\(\perp\)BC(gt)
Do đó: KI//AH(Định lí 1 từ vuông góc tới song song)
Suy ra: \(\widehat{HAI}=\widehat{KIA}\)(hai góc so le trong)(1)
Ta có: ΔABK=ΔIBK(cmt)
nên KA=KI(hai cạnh tương ứng)
Xét ΔKAI có KA=KI(cmt)
nên ΔKAI cân tại K(Định nghĩa tam giác cân)
Suy ra: \(\widehat{KAI}=\widehat{KIA}\)(hai góc ở đáy)(2)
Từ (1) và (2) suy ra \(\widehat{HAI}=\widehat{KAI}\)
\(\Leftrightarrow\widehat{HAI}=\widehat{CAI}\)
Suy ra: AI là tia phân giác của \(\widehat{HAC}\)(Đpcm)
5 tháng 5 2021
a) Xét ΔABK vuông tại A và ΔIBK vuông tại I có
BK chung
\(\widehat{ABK}=\widehat{IBK}\)(BK là tia phân giác của \(\widehat{ABI}\))
Do đó: ΔABK=ΔIBK(Cạnh huyền-góc nhọn)
HN
9 tháng 5 2022
a. Xét Δ ABE và Δ KBE có:
^B1=^B2(BD là tia p/g)
^BEA=^KEB=90o
AE chung
=> ΔABE=ΔKBE(g.c.g)
=>AB=KB
=>ΔABK cân tại B
(xin lỗi mình ko biết phần b,c,d) ;-;
cho bạn cái hình nè :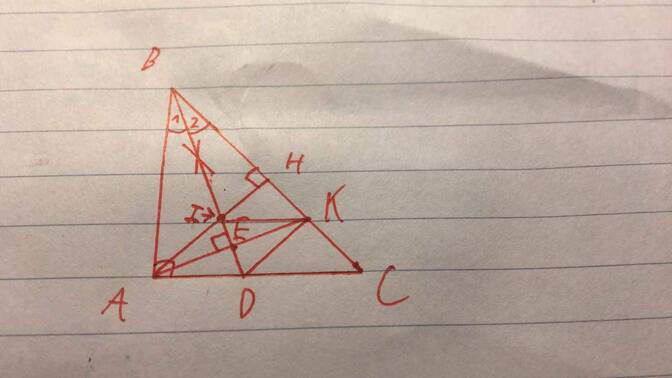
T
9 tháng 7 2020
a.Xét tam giác ABH vuông tại H và góc B = 0độ nên góc BAH = 30độ
Ta có ; góc BAC - góc BAH = góc HAC
\(\Rightarrow\)góc HAC = 90độ - 30độ = 60độ
Ta lại có ; AK là tia pg góc HAC nên
góc HAK = góc KAC = \(\frac{\widehat{HAC}}{2}=\frac{60^0}{2}=30^0\)
Suy ra ; góc HAK = góc BAH
Xét hai tam giác vuông ABH và tam giác vuôngAKH có
góc AHB = góc AHK = 90độ
cạnh AH chung
góc BAH = góc HAK [ theo chứng minh trên ]
Do đó ; tam giác ABH = tam giác AKH [ g.c.g ]
\(\Rightarrow AB=AK\Rightarrow\)tam giác ABK cân [ 1 ]
Vì KE // AC nên góc BEK = góc BAC
mà bài cho góc BAC = 90 độ
\(\Rightarrow\)góc BEK = 90độ
\(\Rightarrow\)KE vuông góc với AB
Ta có
AH và KE là đường cao của tam giác ABK
mà I là giao điểm của AH và KE
Suy ra
I là trực tâm của tam giác ABK
\(\Rightarrow\)BI vuông góc với AK và tam giác ABK cân [ theo 1 ]
Ta có định nghĩa sau
Trong 1 tam giác cân đường cao vừa là trung trực, vừa là trung tuyến và là phân giác
Suy ra ; BI là tia phân giác góc ABK
phần b mk chưa nghĩ ra nhé
Chúc bạn học tốt
7 tháng 8 2021
bn tham khảo tại đây;
https://olm.vn/hoi-dap/detail/256733768368.html
10 tháng 3 2022
a: Xét ΔABK và ΔIBK có
BA=BI
\(\widehat{ABK}=\widehat{IBK}\)
BK chung
Do đó: ΔABK=ΔIBK
Suy ra: \(\widehat{BAK}=\widehat{BIK}=90^0\)
hay KI⊥BC
b: Ta có: \(\widehat{HAI}+\widehat{BIA}=90^0\)
\(\widehat{CAI}+\widehat{BAI}=90^0\)
mà \(\widehat{BIA}=\widehat{BAI}\)
nên \(\widehat{HAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc HAC
5 tháng 1 2018
1.Vì các tia phân giác của các góc B và C cắt nhau tại I
\(\Rightarrow\)I là giao của các đường phân giác trong tam giác
\(\Rightarrow\)AI là tia phân giác của góc A
A
20 tháng 6 2019
1.
Kẻ: \(ID\perp AB;IE\perp BC;IF\perp AC\)
\(\widehat{IDB}=\widehat{IEB}=90^0\)
\(\widehat{DBI}=\widehat{EIB}\left(gt\right)\)
BI cạnh huyền chung
⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\widehat{IEC}=\widehat{IFC}=90^0\)
\(\widehat{ECI}=\widehat{FCI}\left(gt\right)\)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
\(\widehat{IDA}=\widehat{IFA}=90^0\)
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra\(\widehat{DAI}=\widehat{FAI}\) (hai góc tương ứng)
Vậy AI là tia phân giác của \(\widehat{A}\)