Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

I là trọng tâm của ΔABC
=>\(\left\{{}\begin{matrix}x_A+x_B+x_C=3\cdot x_I\\y_A+y_B+y_C=3\cdot y_I\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3+\left(-1\right)+x_C=3\cdot1=3\\-1+2+y_C=3\cdot1=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_C=3-2=1\\y_C=3-1=2\end{matrix}\right.\)
Vậy: C(1;2)
Ta có: A(3;-1); B(-1;2); C(1;2); D(x;y)
=>\(\overrightarrow{AB}=\left(-4;3\right);\overrightarrow{DC}=\left(1-x;2-y\right)\)
ABCD là hình bình hành
=>\(\overrightarrow{AB}=\overrightarrow{DC}\)
=>\(\left\{{}\begin{matrix}1-x=-4\\2-y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\)
Vậy: D(5;-1)
Tâm O của hình bình hành ABCD sẽ là trung điểm của AC
A(3;-1); C(1;2); O(x;y)
=>\(\left\{{}\begin{matrix}x=\dfrac{3+1}{2}=\dfrac{4}{2}=2\\y=\dfrac{-1+2}{2}=\dfrac{1}{2}\end{matrix}\right.\)
Áp dụng công thức trọng tâm:
\(\left\{{}\begin{matrix}x_A+x_B+x_C=3x_I\\y_A+y_B+y_C=3y_I\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_C=3x_I-\left(x_A+x_B\right)=1\\y_C=3y_I-\left(y_A+y_B\right)=2\end{matrix}\right.\)
\(\Rightarrow C\left(1;2\right)\)
Đặt tọa độ D là \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-4;3\right)\\\overrightarrow{DC}=\left(1-x;2-y\right)\end{matrix}\right.\)
ABCD là hình bình hành \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow\left\{{}\begin{matrix}1-x=-4\\2-y=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\) \(\Rightarrow D\left(5;-1\right)\)
Tâm O hình bình hành là trung điểm đường chéo AC nên áp dụng công thức trung điểm:
\(\left\{{}\begin{matrix}x_O=\dfrac{x_A+x_C}{2}=2\\y_O=\dfrac{y_A+y_C}{2}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow O\left(2;\dfrac{1}{2}\right)\)

Tọa độ điểm M là:
\(\left\{{}\begin{matrix}x_M=\dfrac{1+1}{2}=1\\y_M=\dfrac{0+4}{2}=2\end{matrix}\right.\)
Tọa độ điểm N là:
\(\left\{{}\begin{matrix}x_N=\dfrac{1+5}{2}=3\\y_N=\dfrac{4+4}{2}=4\end{matrix}\right.\)
Tọa độ điểm P là:
\(\left\{{}\begin{matrix}x_P=\dfrac{5+7}{2}=6\\y_P=\dfrac{4+0}{2}=2\end{matrix}\right.\)
Tọa độ điểm Q là:
\(\left\{{}\begin{matrix}x_Q=\dfrac{7+1}{2}=4\\y_Q=\dfrac{0+0}{2}=0\end{matrix}\right.\)

Đáp án D.
Mặt phẳng (P) có 1 vecto pháp tuyến n → = ( 6 ; 3 ; - 2 )
Đường thẳng AH qua A và vuông góc vưới (P)
Suy ra phương trình của đường thẳng AH là
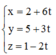
Suy ra H(2+6t; 5+3t; 1-2t)
Mà

Vậy H(-4;2;3)

Đáp án D.
Mặt phẳng (P) có 1 vecto pháp tuyến n → = ( 6 ; 3 ; - 2 )
Đường thẳng AH qua A và vuông góc vưới (P)
Suy ra phương trình của đường thẳng AH là

Suy ra H(2+6t; 5+3t; 1-2t)
Mà

Vậy H(-4;2;3)
