Giải hệ pt;
\(\left\{{}\begin{matrix}xy\left(x+y\right)=x^2-xy+y^2\\\dfrac{1}{x^3}+\dfrac{1}{y^3}=16\end{matrix}\right.\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TC
Trên con đường thành công không có....
27 tháng 7 2021
Đúng(1)
TC
Trên con đường thành công không có....
27 tháng 7 2021
Đúng(1)
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 3 2022
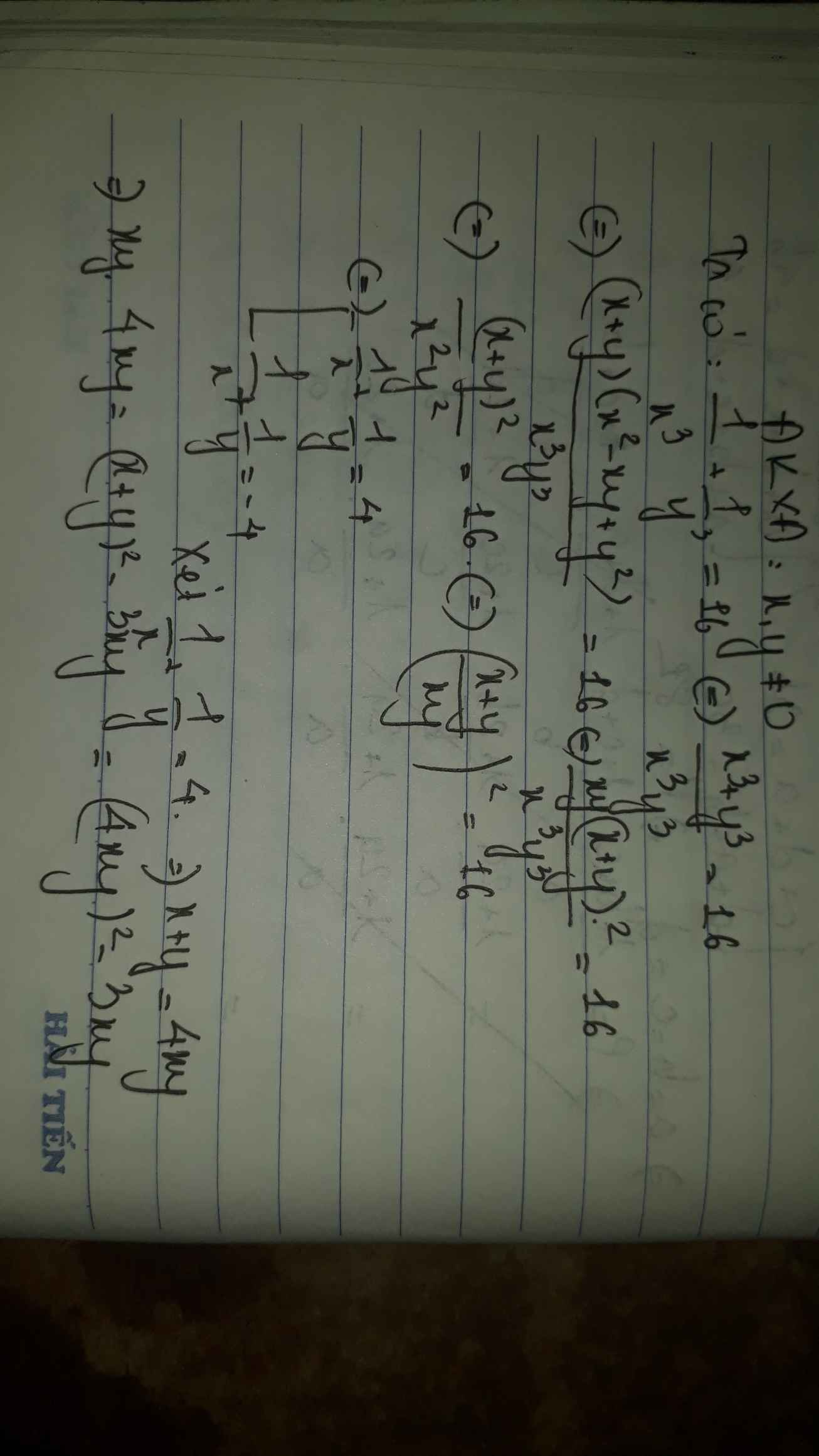
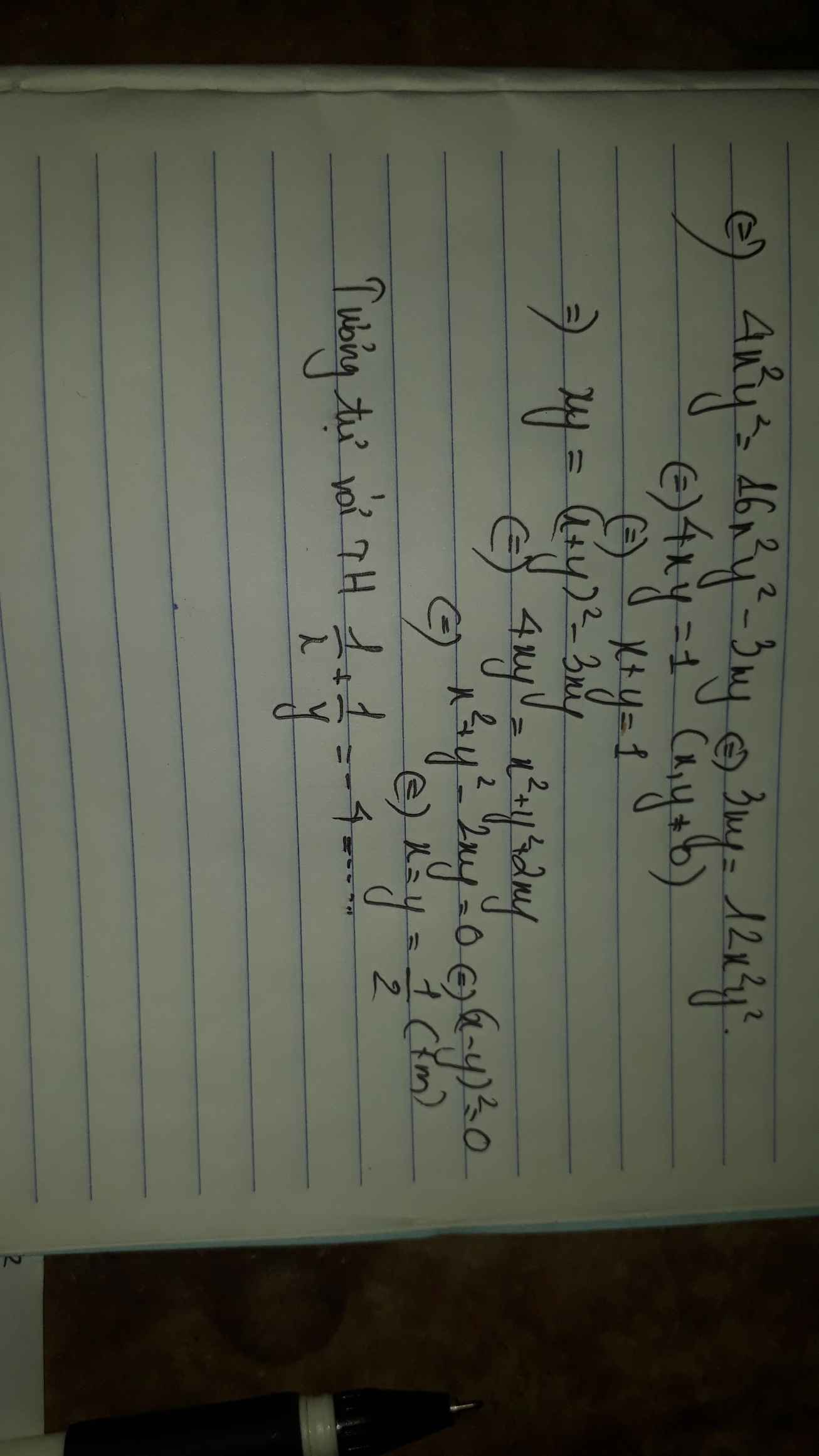
\(\Delta=\left(2m-1\right)^2-8\left(m-1\right)=4m^2-12m+9=\left(2m-3\right)^2\ge0\) ; \(\forall m\)
\(\Rightarrow\) Phương trình đã cho luôn có 2 nghiệm với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-2m+1}{2}\\x_1x_2=\dfrac{m-1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(x_1+x_2\right)=-2m+1\\4x_1x_2=2m-2\end{matrix}\right.\)
Cộng vế với vế:
\(\Rightarrow2\left(x_1+x_2\right)+4x_1x_2=-1\)
Đây là hệ thức liên hệ các nghiệm ko phụ thuộc m
3 tháng 2 2021
Thay m=2 vào HPT ta có:
\(\left\{{}\begin{matrix}\left(2-1\right)x-2y=6-1\\2x-y=2+5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x-2y=5\\2x-y=7\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x-4y=10\\2x-y=7\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x-4y=10\\-3y=3\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)
Vậy HPT có nghiemj (x;y) = (3;-11)
TC
1
20 tháng 11 2023
a: Khi m=2 thì hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}2x+3y=-4\\x-2y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+3y=-4\\2x-4y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7y=-14\\x-2y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-2\\x=2y+5=-4+5=1\end{matrix}\right.\)
b: Để hệ phương trình không có nghiệm thì \(\dfrac{m}{1}=\dfrac{3}{-2}< >-\dfrac{4}{5}\)
=>\(\dfrac{m}{1}=\dfrac{3}{-2}\)
=>\(m=\dfrac{3}{-2}=-\dfrac{3}{2}\)
19 tháng 2 2023
a: x+my=1 và -mx+y=m
Khi m=2 thì x+2y=1 và -2x+y=2
=>x=-3/5; y=4/5
b: 1/-m<>m/1
nên hệ luôn có nghiệm duy nhất
c: x+my=1 và -mx+y=m
=>x=1-my và -m(1-my)+y=m
=>x=1-my và -m+m^2y+y=m
=>x=1-my và y(m^2+1)=-2m
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-2m}{m^2+1}\\x=1-\dfrac{-2m^2}{m^2+1}=\dfrac{m^2+1+2m^2}{m^2+1}=\dfrac{3m^2+1}{m^2+1}\end{matrix}\right.\)
x<1; y<1
=>\(\left\{{}\begin{matrix}\dfrac{-2m}{m^2+1}-1< 0\\\dfrac{3m^2+1-m^2-1}{m^2+1}< 0\end{matrix}\right.\)
=>-2m-m^2-1<0 và 2m^2<0
=>\(m\in\varnothing\)
22 tháng 4 2020
a) Thay m=3 vào hpt \(\hept{\begin{cases}x+y=1\\3x+2y=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=1-x\\3x+2-2x=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\y=0\end{cases}}\)
Vậy m=3 thì hpt có nghiệm duy nhất (x,y)=(1;0)
b)Ta có \(\hept{\begin{cases}x=1-y\\m-my+2y=m\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1-y\left(1\right)\\\left(2-m\right)y=0\left(2\right)\end{cases}}\)
Để hpt có nghiệm duy nhất \(\Leftrightarrow pt\left(2\right)\ne0\Leftrightarrow2-m\ne0\Leftrightarrow m\ne2\)
Khi đó \(\left(2\right)\Leftrightarrow y=0\).Thay vào \(\left(1\right)\Leftrightarrow x=1\)
Để hpt có vô số nghiệm \(\Leftrightarrow2-m=0\Leftrightarrow m=2\)
Vậy m\(\ne\)2 thì hpt có nghiệm duy nhất (x;y)=(1;0)
m=2 thì hpt có vô số nghiệm
LL
10 tháng 4 2021
khi m=2 ta có hệ pt:
\(\left\{{}\begin{matrix}x+2y=2+1\\2x+y=2.2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2y=3\\2x+y=4\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x+4y=6\\2x+y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3y=2\\x+2y=3\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=\dfrac{2}{3}\\2x+\dfrac{2}{3}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2}{3}\\2x=\dfrac{7}{3}\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=\dfrac{2}{3}\\x=\dfrac{5}{3}\end{matrix}\right.\)
vậy khi m=2 thì hệ pt có nghiệm duy nhất\(\left\{\dfrac{2}{3};\dfrac{5}{3}\right\}\)
10 tháng 4 2021
a) Thay m=2 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}x+2y=3\\2x+y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=6\\2x+y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3y=2\\x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2}{3}\\x=3-2y=3-2\cdot\dfrac{2}{3}=\dfrac{5}{3}\end{matrix}\right.\)
Vậy: Khi m=2 thì hệ phương trình có nghiệm duy nhất là \(\left(x,y\right)=\left(\dfrac{5}{3};\dfrac{2}{3}\right)\)
21 tháng 1 2021
b, \(\left\{{}\begin{matrix}x-2y=5\\mx-y=4\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=5+2y\\m\left(5+2y\right)-y=4\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=5+2y\\5m+2my-y=4\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=5+2y\\2my-y=4-5m\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=5+2y\\y\left(2m-1\right)=4-5m\end{matrix}\right.\)
Hpt trên có nghiệm duy nhất \(\Leftrightarrow\) 2m - 1 \(\ne\) 0 \(\Leftrightarrow\) m \(\ne\) \(\dfrac{1}{2}\)
Khi đó ta có hpt:
\(\left\{{}\begin{matrix}x=5+2y\\y=\dfrac{4-5m}{2m-1}\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=5+2.\dfrac{4-5m}{2m-1}\\y=\dfrac{4-5m}{2m-1}\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=\dfrac{3}{2m-1}\\y=\dfrac{4-5m}{2m-1}\end{matrix}\right.\)
Vậy với m \(\ne\) \(\dfrac{1}{2}\) thì hpt trên có nghiệm duy nhất \(\left\{{}\begin{matrix}x=\dfrac{3}{2m-1}\\y=\dfrac{4-5m}{2m-1}\end{matrix}\right.\)
Vì x, y trái dấu nên ta xét 2 trường hợp
Th1: x > 0; y < 0
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}\dfrac{3}{2m-1}>0\\\dfrac{4-5m}{2m-1}< 0\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}2m-1>0\\4-5m< 0\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}m>\dfrac{1}{2}\\m>\dfrac{4}{5}\end{matrix}\right.\)
\(\Leftrightarrow\) m > \(\dfrac{4}{5}\) (Thỏa mãn)
Th2: x < 0; y > 0
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}\dfrac{3}{2m-1}< 0\\\dfrac{4-5m}{2m-1}>0\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}2m-1< 0\\4-5m< 0\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}m< \dfrac{1}{2}\\m>\dfrac{4}{5}\end{matrix}\right.\)
\(\Leftrightarrow\) \(\dfrac{4}{5}< m< \dfrac{1}{2}\) (Vô lý)
Vậy m > \(\dfrac{4}{5}\) thì hpt có nghiệm duy nhất và thỏa mãn x, y trái dấu
c, Từ b ta có:
Với x \(\ne\) \(\dfrac{1}{2}\) hpt có nghiệm duy nhất \(\left\{{}\begin{matrix}x=\dfrac{3}{2m-1}\\y=\dfrac{4-5m}{2m-1}\end{matrix}\right.\)
Vì x = |y| \(\Leftrightarrow\) \(\dfrac{3}{2m-1}=\left|\dfrac{4-5m}{2m-1}\right|\)
Xét các trường hợp:
Th1: \(\dfrac{3}{2m-1}=\dfrac{4-5m}{2m-1}\)
\(\Leftrightarrow\) 3 = 4 - 5m (Vì m \(\ne\) \(\dfrac{1}{2}\))
\(\Leftrightarrow\) 5m = 1
\(\Leftrightarrow\) m = \(\dfrac{1}{5}\) (TM)
Th2: \(\dfrac{3}{2m-1}=\dfrac{5m-4}{2m-1}\)
\(\Leftrightarrow\) 3 = 5m - 4 (Vì m \(\ne\) \(\dfrac{1}{2}\))
\(\Leftrightarrow\) 5m = 7
\(\Leftrightarrow\) m = \(\dfrac{7}{5}\) (TM)
Vậy với m = \(\dfrac{1}{5}\); m = \(\dfrac{7}{5}\) thì hpt có nghiệm duy nhất và thỏa mãn x = |y|
Chúc bn học tốt!
AH
Akai Haruma
Giáo viên
22 tháng 12 2021
Lời giải:
Đặt $x-y=a; xy=b$ thì hpt trở thành:
\(\left\{\begin{matrix}
x-y+2xy=5\\
(x-y)^2+3xy=7\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
a+2b=5\\
a^2+3b=7\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
3a+6b=15\\
2a^2+6b=14\end{matrix}\right.\)
\(\Rightarrow 2a^2-3a=-1\)
$\Leftrightarrow 2a^2-3a+1=0$
$\Leftrightarrow (a-1)(2a-1)=0$
$\Rightarrow a=1$ hoặc $a=\frac{1}{2}$
Nếu $a=1$ thì $b=2$. Khi đó: $x-y=1; xy=2$ nên theo định lý Viet đảo thì $x,-y$ là nghiệm của pt:
$X^2-X-2=0$
$\Rightarrow (x,-y)=(2,-1), (-1,2)\Rightarrow (x,y)=(2,1), (-1,-2)$
Nếu $a=\frac{1}{2}$ thì $b=\frac{9}{4}$. Khi đó theo định lý Viet đảo thì $x,-y$ là nghiệm của pt:
$X^2-\frac{1}{2}X-\frac{9}{4}=0$
$\Rightarrow (x,-y)=(\frac{1+\sqrt{37}}{4}, \frac{1-\sqrt{37}}{4}), (\frac{1-\sqrt{37}}{4}, \frac{1+\sqrt{37}}{4})$
$\Rightarrow (x,y)= (\frac{1+\sqrt{37}}{4}, \frac{-1+\sqrt{37}}{4}), (\frac{1-\sqrt{37}}{4}, \frac{-1-\sqrt{37}}{4})$
AH
Akai Haruma
Giáo viên
22 tháng 12 2021
Lần sau bạn lưu ý không đăng 1 bài nhiều lần. Nếu bạn còn đăng vậy lần nữa sẽ bị tính là spam và bị xóa không thương tiếc đó nhé.