
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TL:
\(B=2x^2+y^2-2xy-2x+3\)
\(=\left(x^2-2xy+y^2\right)+(x^2-2x+1)+2\)
\(=\left(x-y\right)^2+\left(x-1\right)^2+2\ge2\forall x;y\)
\(D=\left(x+8\right)^4+\left(x+6\right)^4\ge0\forall x\)
Dấu"=" xảy ra<=> \(\hept{\begin{cases}\left(x+8\right)^4=0\\\left(x+6\right)^4=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=-8\\x=-6\end{cases}}\)

Mình làm một câu để bạn tham khảo, sau đó bạn áp dụng làm các bài còn lại nha ^^
Có gì không hiểu bạn ib nha ^^
1. \(2x=3y-2x\left(1\right)\) và \(x+y=14\)
\(\left(1\right)\Leftrightarrow4x=3y\)
\(\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{4}\)
Theo tính chất dãy tỉ số bằng nhau, có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{x+y}{3+4}=\dfrac{14}{7}=2\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2.3=6\\y=2.4=8\end{matrix}\right.\)
Bạn tự kết luận ^^

* a mũ 2 hay 4 hay 6 ,... ( những số tự nhiên chẵn khác 0 ) đều lớn hơn hoặc bằng 0 với mọi a
Áp dụng :
a) (2x-8)^4 + (3y+45)^2 = 0
Vì : (2x-8)^4 >=0 , (3y+45)^2 >=0 với mọi x,y
=> (2x-8)^4 + (3y+45)^2 >=0
Dấu "=" xảy ra khi : 2x-8=3y+45=0
->(x;y)=(4;-15)
Những câu sau làm tương tự, ta được :
b) ...
Dấu "=" xảy ra khi : 2x-10=0 và x+y-7=0
->x=5 và 5+y-7=0
->(x;y)=(5;2)
c) 5x-15=0 và 2x-y+4=0
->x=3 và 6-y+4=0
->(x;y)=(3;10)
d) Trùng câu a

\(2x+3y-xy=8\)
\(\Rightarrow2x+3y-xy-6=2\)
\(\Rightarrow x\left(2-y\right)-3\left(2-y\right)=2\)
\(\Rightarrow\left(x-3\right)\left(2-y\right)=2\)

\(3x^2-2x-8=0\\ \Leftrightarrow3x^2-2x=8\\ E=6x^2-4x+9\\ =3x^2+3x^2-2x-2x-8+17\\ =\left(3x^2-2x-8\right)+\left(3x^2-2x+17\right)\\ =3x^2-2x+17\\ =\left(3x^2-2x\right)+17=8+17=25\)
\(x+y=0\\ \Leftrightarrow y=-x\\ D=x^4-y^4+x^3y-xy^3\\ =\left(x^2+y^2\right)\left(x^2-y^2\right)+xy\left(x^2-y^2\right)\\ =\left(x^2+y^2+xy\right)\left(x^2-y^2\right)\\ =\left(x^2+\left(-x\right)^2+x.\left(-x\right)\right)\left(x^2-\left(-x\right)^2\right)\\ =\left(x^2+x^2-x^2\right)\left(x^2-x^2\right)\\ =x^2.0=0\)

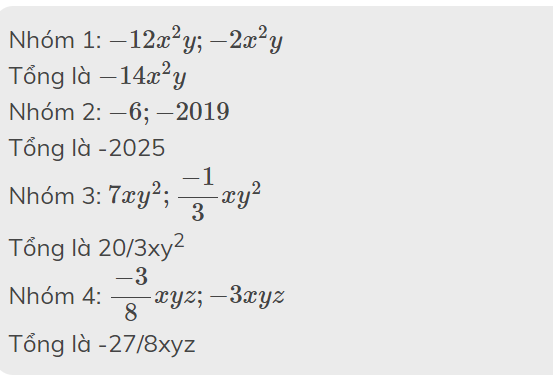
đề là gì vậy
Tìm Xy ok