K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 12 2021
\(a,\) Vì AH la đường cao tg ABC cân A nên AH cũng là trung tuyến
Mà H là trung điểm AE nên ABEC là hbh
Mà AE vuông BC tại H nên ABEC là hthoi
\(b,\) Theo tc trung tuyến ứng cạnh huyền thì \(HI=\dfrac{1}{2}AC\)
Vì D,F là trung điểm AH,HC nên DF là đtb
Do đó \(DF=\dfrac{1}{2}AC\)
Vậy \(DF=HI\)
NL
4 tháng 4 2018
mình tìm không tháy bạn ơi ~ chủ yếu là mình nhờ mấy bạn từng học qua rồi chỉ giúp những dạng chủ yếu,mẹo vặt các loại đấy bạn !! không phải mình tìm đề đâu ~~`
NL
1
16 tháng 2 2022
a, \(3x+7x^2+5+2x-7x^2\ge0\Leftrightarrow5x+5\ge0\Leftrightarrow x\ge-1\)
b, \(12x\ge-16\Leftrightarrow x\ge-\dfrac{4}{3}\)
c, \(\dfrac{5x-1-6}{6}-\dfrac{4\left(x+1\right)}{3}\le0\)
\(\Leftrightarrow\dfrac{5x-7-8\left(x+1\right)}{6}\le0\Rightarrow-3x-15\le0\Leftrightarrow x\le-5\)
DT
Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ
2
10 tháng 12 2023
a: Xét tứ giác ABQN có
\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)
=>ABQN là hình chữ nhật
b: Xét ΔCAD có
DN,CH là các đường cao
DN cắt CH tại M
Do đó: M là trực tâm của ΔCAD
=>AM\(\perp\)CD
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
=>\(HA=\sqrt{HB\cdot HC}\)
S
1
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 4 2022
80cm=0,8m, 60cm=0,6m
Diện tích xung quanh căn phòng là:
\(2\left(10+5\right).4=120\left(m^2\right)\)
Diện tích cửa chính:
\(1,8\times2=3,6\left(m^2\right)\)
Diện tích 2 cửa sổ:
\(0,8\times0,6\times2=0,96\left(m^2\right)\)
Diện tích cần sơn:
\(200-\left(3,6+0,96\right)=115,44\left(m^2\right)\)
Chi phí tiền công:
\(195,44\times25000=2886000\) đồng
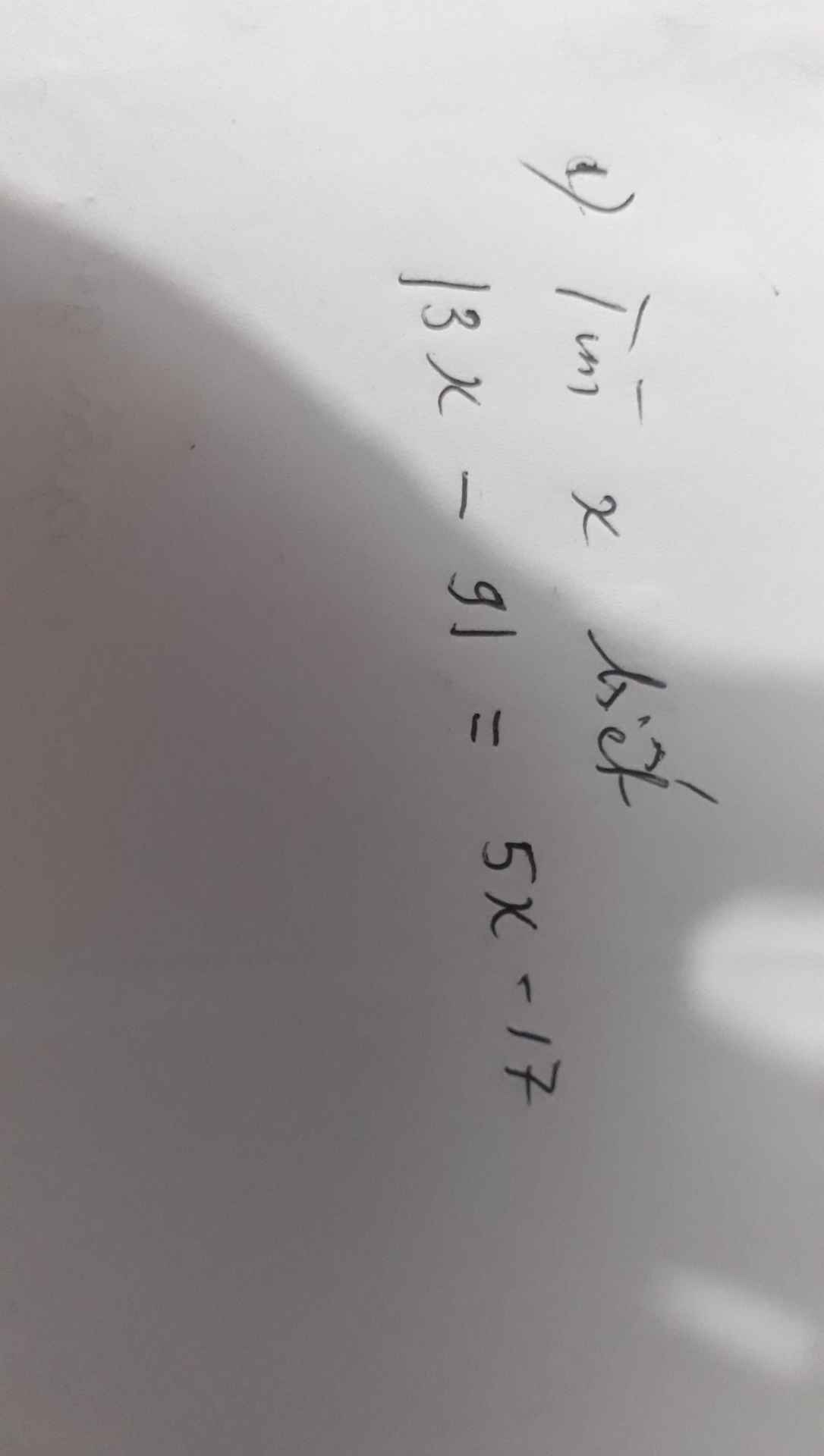
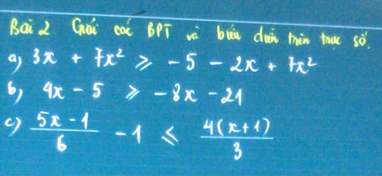
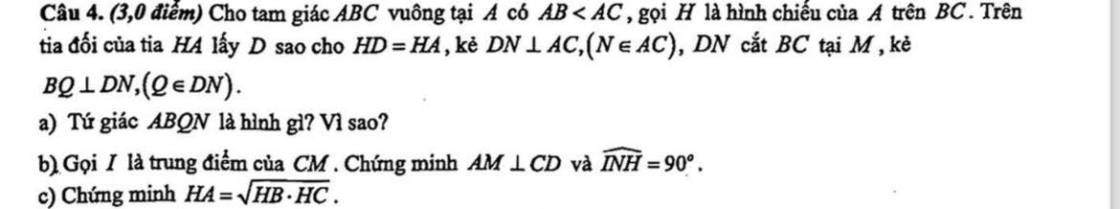
a. \(\widehat{DAB}=\widehat{ABC}=\widehat{BCE}=90^0\)
\(\widehat{ABD}=180^0-\widehat{ABC}-\widehat{EBC}=180^0-60^0-\left(180^0-\widehat{BCE}-\widehat{CEB}\right)=180^0-60^0-\left(180^0-60-\widehat{CEB}\right)=\widehat{CEB}\)\(\Rightarrow\)△ABD∼△CEB (g-g).
\(\Rightarrow\dfrac{AD}{CB}=\dfrac{AB}{CE}\Rightarrow AD.CE=CB.AB\Rightarrow AD.CE=a^2\) không đổi
b. \(\widehat{CAD}=\widehat{BAD}+\widehat{BAC}=60^0+60^0=\widehat{BCE}+\widehat{ACB}=\widehat{ACE}\)
\(\dfrac{AD}{CB}=\dfrac{AB}{CE}\Rightarrow\dfrac{AD}{AC}=\dfrac{AC}{CE}\)
\(\Rightarrow\)△ACD∼△CEA (c-g-c)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ACD}=\widehat{CEA}\\\dfrac{CE}{AC}=\dfrac{EA}{CD}\end{matrix}\right.\)
\(\Rightarrow\)△ACK∼△AEC (g-g).
\(\Rightarrow\dfrac{CK}{EC}=\dfrac{AK}{AC}\Rightarrow\dfrac{CE}{AC}=\dfrac{CK}{AK}\)
\(\Rightarrow\dfrac{AE}{CD}=\dfrac{CK}{AK}\Rightarrow AE.AK=CD.CK\)