Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Gọi V0 là thể tích của khối lập phương ở 0oC:
V0 = l03
+ V là thể tích của khối lập phương ở t0C:
V = l3 = [l0(1+ α∆t)]3 = l03 (1+α∆t)3
Mà (1+ α∆t)3 = 1 + 3α∆t + 3α2∆t2 + α3∆t3
Vì α khá nhỏ nên α2, α3 có thể bỏ qua.
=> V = l3 = l03 (1+ 3α∆t) = Vo (1+ β∆t) với β = 3α.

Ta có: ∆ S = S - S 0 = β ' S 0 ∆ t = 2 α S 0 ∆ t
=>Độ tăng diện tich tỉ đối: ∆ S S 0 = β ' ∆ t = 2 α ∆ t = 2 . 24 . 10 - 6 . 100 = 4 , 8 . 10 - 3 = 0 , 48 %
Đáp án: B

Ta có: Độ nở khối: ∆ V = V - V 0 = β V 0 ∆ t = 3 α V 0 ∆ t
→ V - V 0 V 0 = 3 α ∆ t
Đáp án: B

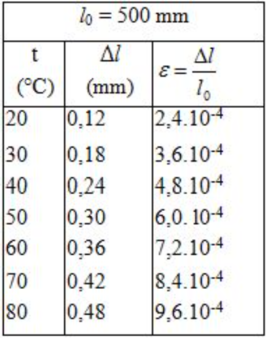
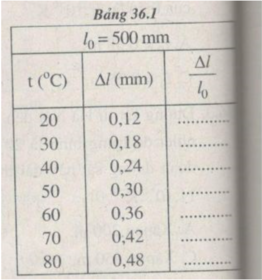
Hình 36.1G có dạng đoạn thẳng.
Điều này chứng tỏ độ biến dạng tỉ đối ∆ l/ l 0 của thanh sắt tỉ lệ thuận với độ tăng nhiệt độ t (tính từ 0 ° C):
∆ l/ l 0 = α t
Nhận xét thấy hệ số tỉ lệ α chính là hệ số nở dài của thép.
Hệ số tỉ lệ α được xác định bởi hệ số góc của đường biểu diễn đồ thị ở Hình 36.1G.

Kết quả tính độ dãn dài tỉ đối của thanh thép ở những nhiệt độ t khác nhau (được ghi ở bảng bên)

Chọn tỉ xích trên các trục toạ độ :
Trục hoành : 1 cm → t = 10 ° C.
Trục tung : 1 cm → = 1,2. 10 - 4
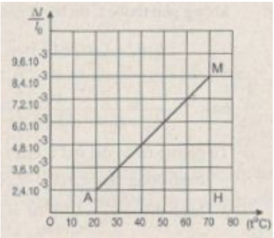
Đường biểu diễn đồ thị vẽ được trên

Độ nở khối (thể tích) của sắt được tính theo công thức :
∆ V = V 0 β ∆ t = V 0 3 α ∆ t
với V0 là thể tích của khối sắt ở 0 ° C, β = 3 α là hệ số nở khối của sắt, còn độ tăng nhiệt độ Δt của khối sắt liên hệ với lượng nhiệt Q mà khối sắt đã hấp thụ khi bị nung nóng bởi công thức :
Q = cm ∆ t ≈ cD V 0 ∆ t với c là nhiột dung riêng, D là khối lượng riêng và m là khối lượng của sắt. Vì D = D 0 ( 1 + β t), nhưng β t << 1 nên coi gần đúng : m = D 0 V 0 ≈ D V 0
Từ đó suy ra: ∆ V = 3 α Q/cD
Thay số ta được:
![]()

Chọn D.
Chất rắn vô định hình không có cấu trúc tinh thể, do đó không có dạng hình học xác định, không có nhiệt độ nóng chảy (hoặc đông đặc) xác định và có tính đẵng hướng.
Ở nhiệt độ t0 (ºC) cạnh hình lập phương là l0
→ thể tích khối lập phương là:
Ở nhiệt độ t (ºC) cạnh hình lập phương là l
→ thể tích khối lập phương là: V = l3
Mặt khác ta có: l = l0.(1 + αΔt) ⇒ V = l03.(1 + αΔt)3
Do α rất nhỏ nên α2 và α3 cũng rất nhỏ, ta có thể bỏ qua.
→ ΔV = V – V0 = V0.β.Δt