Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đồ thị hàm số \(y = a{x^2} + bx + 1\) đi qua điểm A(1; 0) nên:
\(a{.1^2} + b.1 + 1 = 0 \Leftrightarrow a + b = - 1\)
Đồ thị hàm số \(y = a{x^2} + bx + 1\) đi qua điểm B(2; 4) nên:
\(a{.2^2} + 2b + 1 = 4 \Leftrightarrow 4a + 2b = 3\)
Từ 2 phương trình trên, ta có \(a = \frac{5}{2};b = \frac{{ - 7}}{2}\)
=> Hàm số cần tìm là \(y = \frac{5}{2}{x^2} - \frac{7}{2}x + 1\)
b) Đồ thị hàm số \(y = a{x^2} + bx + 1\) đi qua điểm A(1; 0) nên:
\(a{.1^2} + b.1 + 1 = 0 \Leftrightarrow a + b = - 1\)
Đồ thị hàm số \(y = a{x^2} + bx + 1\) có trục đối xứng x=1
\(\frac{{ - b}}{{2a}} = 1 \Leftrightarrow - b = 2a \Leftrightarrow 2a + b = 0\)
Từ 2 phương trình trên, ta có \(a = 1;b = - 2\)
=> Hàm số cần tìm là \(y = {x^2} - 2x + 1\)
c) Đồ thị hàm số \(y = a{x^2} + bx + 1\) có đỉnh \(I(1;2)\) nên:
\(\frac{{ - b}}{{2a}} = 1 \Leftrightarrow - b = 2a \Leftrightarrow 2a + b = 0\)
\(a{.1^2} + b.1 + 1 = 2 \Leftrightarrow a + b = 1\)
Từ 2 phương trình trên, ta có \(a = - 1;b = 2\)
=> Hàm số cần tìm là \(y = - {x^2} + 2x + 1\)
d) Đồ thị hàm số \(y = a{x^2} + bx + 1\) đi qua điểm C(-1; 1) nên:
\(a.{( - 1)^2} + b.( - 1) + 1 = 1 \Leftrightarrow a - b = 0 \Leftrightarrow a = b\)
Đồ thị hàm số \(y = a{x^2} + bx + 1\) có tung độ đỉnh là -0,25 nên:
\(\frac{{ - \Delta }}{{4a}} = - 0,25 \Leftrightarrow - \frac{{{b^2} - 4.a.1}}{{4a}} = - 0,25 \Leftrightarrow {b^2} - 4a = a \Leftrightarrow {b^2} = 5a\)
Thay a=b ta có:
\({b^2} = 5b \Leftrightarrow b=0\) hoặc \(b=5\)
Vì \(a \ne 0\) nên \(a=b=5\)
=> Hàm số cần tìm là \(y = 5{x^2} + 5x + 1\)

a) Vì parabol đi qua M(1; 5) nên tọa độ của M nghiệm đúng phương trình của parabol: 5 = a.12 + b.1 + 2.
Tương tự, với N(- 2; 8) ta có: 8 = a.(- 2)2 + b.(- 2) + 2
Giải hệ phương trình: ta được a = 2, b = 1.
Parabol có phương trình là: y = 2x2 + x + 2.
b) Giải hệ phương trình:
Parabol: y = x2 - x + 2.
c) Giải hệ phương trình:
Parabol: y = x2 - 4x + 2.
d) Ta có:
Parabol: y = 16x2 + 12x + 2 hoặc y = x2 - 3x + 2.

(P) : y = ax2 + bx + c
Parabol có đỉnh I(1 ; 4) ⇒ –b/2a = 1 ⇒ b = –2a ⇒ 2a + b = 0.
Parabol đi qua I(1; 4) ⇒ 4 = a.12 + b . 1 + c ⇒ a + b + c = 4.
Paraol đi qua D(3; 0) ⇒ 0 = a.32 + b.3 + c ⇒ 9a + 3b + c = 0.
Giải hệ phương trình 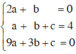
ta được : a = –1 ; b = 2 ; c = 3.
Vậy a = –1 ; b = 2 ; c = 3.

a) Thay tọa độ điểm \(M\left( {1;12} \right)\) và \(N\left( { - 3;4} \right)\) ta được:
\(\begin{array}{l}\left\{ \begin{array}{l}a{.1^2} + b.1 + 4 = 12\\a.{\left( { - 3} \right)^2} + b.\left( { - 3} \right) + 4 = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a + b = 8\\9a - 3b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 6\end{array} \right.\end{array}\)
Vậy parabol là \(y = 2{x^2} + 6x + 4\)
b) Hoành độ đỉnh của parabol là \(x_I = \frac{{ - b}}{{2a}}\)
Suy ra \(x_I = \frac{{ - b}}{{2a}} = - 3 \Leftrightarrow b = 6a\) (1)
Thay tọa độ điểm I vào ta được:
\(\begin{array}{l} - 5 = a.{\left( { - 3} \right)^2} + b.\left( { - 3} \right) + 4\\ \Leftrightarrow 9a - 3b = - 9\\ \Leftrightarrow 3a - b = - 3\left( 2 \right)\end{array}\)
Từ (1) và (2) ta được hệ
\(\begin{array}{l}\left\{ \begin{array}{l}b = 6a\\3a - b = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 6a\\3a - 6a = - 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}b = 6a\\a = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 6\\a = 1\end{array} \right.\end{array}\)
Vậy parabol là \(y = {x^2} + 6x + 4\).

Vì parabol đi qua ba điểm A, B, C nên ta có hệ phương trình:
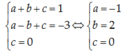
Vậy (P): y = -x2 + 2x
Chọn C.

a) Theo giả thiết, hai điểm \(A(1;1)\) và \(B( - 1;0)\) thuộc parabol \(\left( P \right):y = a{x^2} + bx + 3\) nên ta có: \(\left\{ {\begin{array}{*{20}{c}}{a + b + 3 = 1}\\{a - b + 3 = 0}\end{array}\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{a = \frac{{ - 5}}{2}}\\{b = \frac{1}{2}}\end{array}} \right.} \right.\)
Vậy hàm số cần tìm là: \(y = - \frac{5}{2}{x^2} + \frac{1}{2}x + 3.\)
b) Parabol nhận \(x = 1\) làm trục đối xứng nên \( - \frac{b}{{2a}} = 1\,\, \Leftrightarrow \,\,b = - 2a.\)
Điểm \(M(1;2)\) thuộc parabol nên \(a + b + 3 = 2\,\, \Leftrightarrow \,\,a + b = - 1.\)
Do đó, ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{b = - 2a}\\{a + b = - 1}\end{array}\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = - 2}\end{array}} \right.} \right.\)
Vậy hàm số cần tìm là: \(y = {x^2} - 2x + 3\)
c) Parabol có đỉnh \(I(1;4)\) nên ta có:
\(\left\{ {\begin{array}{*{20}{c}}{ - \frac{b}{{2a}} = 1}\\{a + b + 3 = 4}\end{array}\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{b = - 2a}\\{a + b = 1}\end{array}\,\, \Leftrightarrow \,\,} \right.} \right.\left\{ {\begin{array}{*{20}{c}}{a = - 1}\\{b = 2}\end{array}} \right.\)
Vậy hàm số cần tìm là: \(y = - {x^2} + 2x + 3.\)

Lời giải:
ĐK: $a\neq 0$
Gọi đỉnh của parabol là $I$.
Ta có:
Hoành độ đỉnh: $x_I=\frac{-b}{2a}$
Tung độ đỉnh: $y_I=ax_I^2+bx_I+1=1-\frac{b^2}{4a}=0$
$\Rightarrow b^2=4a(*)$
Mặt khác parabol đi qua điểm $N(1,4)$ nên:
$y_N=ax_N^2+bx_N+1$
$\Leftrightarrow 4=a+b+1(**)$
Từ $(*); (**)\Rightarrow b^2=4(3-b)\Rightarrow b=2$ hoặc $b=-6$
Nếu $b=2\rightarrow a=1$. Parabol $y=x^2+2x+1$
Nếu $b=-6\rightarrow a=9$. Parabol $y=9x^2-6x+1$