Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) \(\dfrac{x-y}{-2}< x+y+1\)
\(\Leftrightarrow x-y>-2x-2y-2\)
\(\Leftrightarrow3x+y+2>0\)
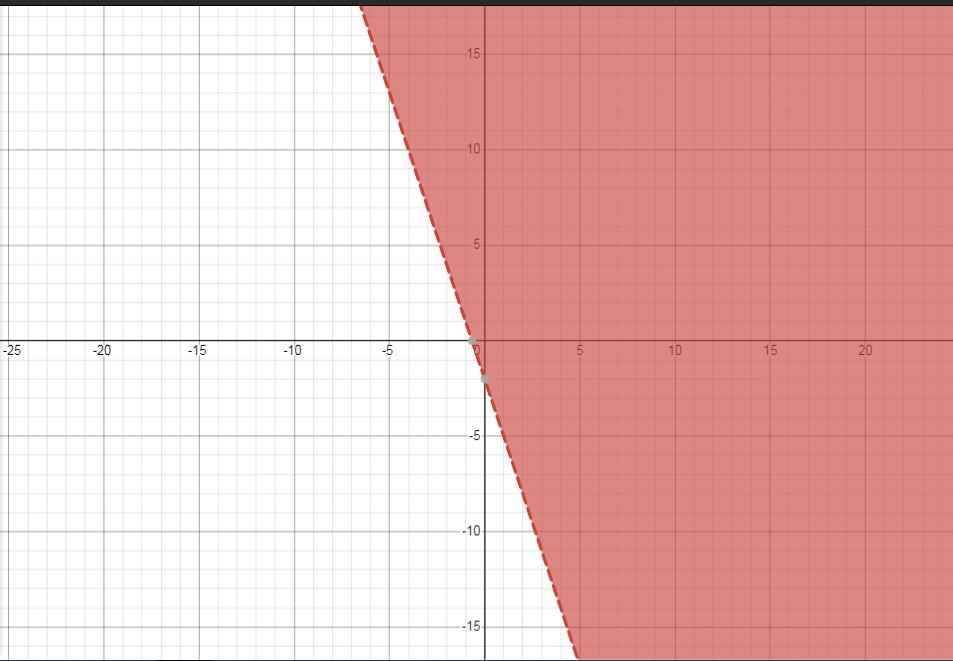

\(\dfrac{x-2y}{2}>\dfrac{2x+y+1}{3}\\ < =>3\left(x-2y\right)>2\left(2x+y+1\right)\\ < =>3x-6y>4x+2y+2\\ < =>4x-3x+2y+6y< -2\\ < =>x+8y< -2\)
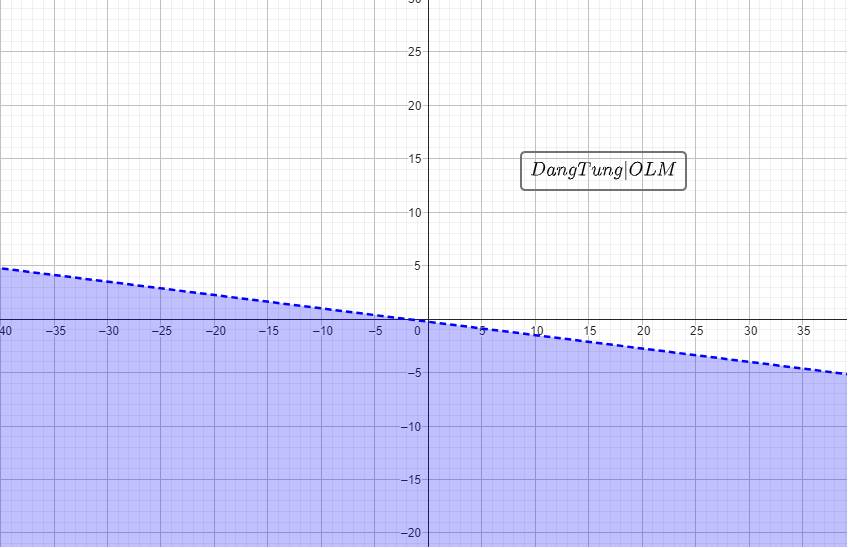

\(\begin{array}{l}\dfrac{{x + y}}{2} \ge \dfrac{{2x - y + 1}}{3}\\ \Leftrightarrow 3\left( {x + y} \right) \ge 2\left( {2x - y + 1} \right)\\ \Leftrightarrow 3x + 3y \ge 4x - 2y + 2\\ \Leftrightarrow x - 5y \le - 2\end{array}\)
Biểu diễn miền nghiệm của bất phương trình:
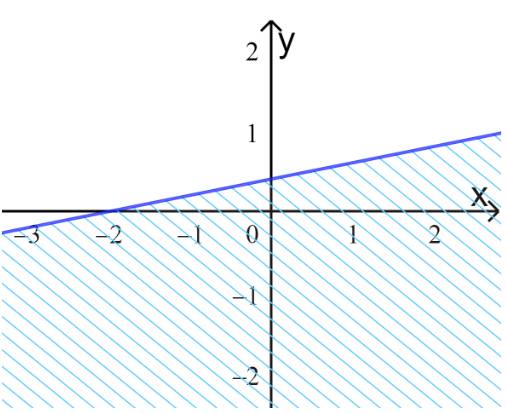
Bước 1: Vẽ đường thẳng d:\(x - 5y = - 2\) (nét liền) đi qua A(-2;0) và B(0;0,4)
Bước 2: Lấy tọa độ điểm O(0;0) thay vào biểu thức x-5y ta được: x-5y=0-5.0=0>-2
=> Điểm O không thuộc miền nghiệm của bất phương trình.
Vậy miền nghiệm của BPT đã cho là nửa mặt phẳng có bờ là đường thẳng d:\(x - 5y = - 2\) và không chứa gốc tọa độ O.

1) \(ĐK:x\ne2\)
Nếu \(x>2\)
BPT ⇔ \(x^2-2x+5-\left(x-1\right)\left(x-2\right)\ge0\) ⇔ \(x^2-2x+5-\left(x^2-3x+3\right)\ge0\)
⇔\(x+2\ge0\) ⇔\(x\ge-2\) ⇒ Lấy \(x\ge2\)
Nếu \(x< 2\)
BPT ⇔\(\dfrac{-\left(x^2-2x+5\right)}{x-2}-x+1\ge0\) ⇔\(-x^2+2x-5-\left(x-1\right)\left(x-2\right)\ge0\)
⇔\(-x^2+2x-5-x^2+3x-2\ge0\)
⇔\(-2x^2+5x-7\ge0\)
⇔\(x^2-\dfrac{5}{2}x+\dfrac{7}{2}\le0\)
⇔\(\left(x-\dfrac{5}{4}\right)^2\le\dfrac{11}{4}\)
⇔\(\left[{}\begin{matrix}x-\dfrac{5}{4}\le\dfrac{11}{4}\\x-\dfrac{5}{4}\le\dfrac{-11}{4}\end{matrix}\right.\) ⇔\(\left[{}\begin{matrix}x\le4\\x\le\dfrac{-3}{2}\end{matrix}\right.\) ⇔ \(x\le\dfrac{-3}{2}\)
S= [2;+∞)U(-∞;\(\dfrac{-3}{2}\)]
2) \(ĐK:x\ne-1\)
Nếu \(x>-1\)
BPT ⇔ \(2x-3-2\left(x+1\right)< 0\) ⇔\(2x-3-2x-2< 0\)
⇔\(-5< 0\) ( luôn đúng với mọi \(x>-1\))
Nếu \(x< -1\)
BPT⇔\(\dfrac{-\left(2x-3\right)}{x+1}-2< 0\) ⇔\(-\left(2x-3\right)-2\left(x+1\right)< 0\) ⇔\(-4x+1< 0\) ⇔ \(x>\dfrac{-1}{4}\)
Vậy S=....

1.
ĐK: \(x\ne7;x\ne-1;x\ne3\)
\(\dfrac{2x-5}{x^2-6x-7}\le\dfrac{1}{x-3}\left(1\right)\)
TH1: \(x< -1\)
\(\left(1\right)\Leftrightarrow\left(2x-5\right)\left(x-3\right)\ge x^2-6x-7\)
\(\Leftrightarrow2x^2-11x+15\ge x^2-6x-7\)
\(\Leftrightarrow x^2-5x+22\ge0\)
\(\Leftrightarrow\) Bất phương trình đúng với mọi \(x< -1\)
TH2: \(-1< x< 3\)
\(\left(1\right)\Leftrightarrow\left(3-x\right)\left(2x-5\right)\ge\left(7-x\right)\left(x+1\right)\)
\(\Leftrightarrow-2x^2+11x-15\ge-x^2+6x+7\)
\(\Leftrightarrow-x^2+5x-22\ge0\)
\(\Rightarrow\) vô nghiệm
TH3: \(3< x< 7\)
Khi đó \(\dfrac{2x-5}{x^2-6x-7}\le0\); \(\dfrac{1}{x-3}>0\)
\(\Rightarrow\) Bất phương trình đúng với mọi \(3< x< 7\)
TH4: \(x>7\)
\(\left(1\right)\Leftrightarrow\left(2x-5\right)\left(x-3\right)\le x^2-6x-7\)
\(\Leftrightarrow2x^2-11x+15\le x^2-6x-7\)
\(\Leftrightarrow x^2-5x+22\le0\)
\(\Rightarrow\) vô nghiệm
Vậy ...
Các bài kia tương tự, chứ giải ra mệt lắm.

\(\dfrac{2x-1}{x+1}-2< 0.\left(x\ne-1\right).\\ \Leftrightarrow\dfrac{2x-1-2x-2}{x+1}< 0.\Leftrightarrow\dfrac{-3}{x+1}< 0.\)
Mà \(-3< 0.\)
\(\Rightarrow x+1>0.\Leftrightarrow x>-1\left(TMĐK\right).\)
\(\dfrac{x^2-2x+5}{x-2}-x+1\ge0.\left(x\ne2\right).\\ \Leftrightarrow\dfrac{x^2-2x+5-x^2+2x+x-2}{x-2}\ge0.\\ \Leftrightarrow\dfrac{x+3}{x-2}\ge0.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+3\ge0.\\x-2\ge0.\end{matrix}\right.\\\left\{{}\begin{matrix}x+3\le0.\\x-2\le0.\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge-3.\\x\ge2.\end{matrix}\right.\\\left\{{}\begin{matrix}x\le-3.\\x\le2.\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge2.\\x\le-3.\end{matrix}\right.\)
Kết hợp ĐKXĐ.
\(\Rightarrow\left[{}\begin{matrix}x>2.\\x\le-3.\end{matrix}\right.\)
\(\dfrac{\left(1+2x\right)\left(x-2\right)}{\left(2x+3\right)\left(1-x\right)}\le0.\left(x\ne1;x\ne\dfrac{-3}{2}\right).\)
Đặt \(\dfrac{\left(1+2x\right)\left(x-2\right)}{\left(2x+3\right)\left(1-x\right)}=f\left(x\right).\)
Ta có bảng sau:
| \(x\) | \(-\infty\) \(-\dfrac{3}{2}\) \(-\dfrac{1}{2}\) \(1\) \(2\) \(+\infty\) |
| \(1+2x\) | - | - 0 + | + | + |
| \(x-2\) | - | - | - | - 0 + |
| \(2x+3\) | - 0 + | + | + | + |
| \(1-x\) | + | + | + 0 - | - |
| \(f\left(x\right)\) | - || + 0 - || + 0 - |
Vậy \(f\left(x\right)\ge0.\Leftrightarrow x\in\left(\dfrac{-3}{2};\dfrac{-1}{2}\right)\cup\)(1;2].

a) <=>
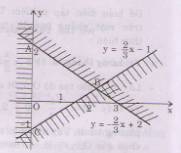
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
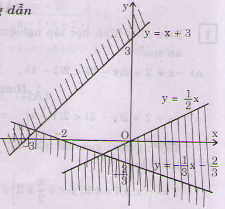
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).

Tham khảo:
a) Ta vẽ đường thẳng d’:\(x + 2y = 3 \Leftrightarrow y = - \frac{x}{2} + \frac{3}{2}\)
Thay tọa độ điểm O(0;0) vào bất phương trình \(x + 2y < 3\) ta được:
\(0 + 2.0 = 0 < 3\) (Luôn đúng)
Vậy O nằm trong miền nghiệm.
Ta có miền nghiệm:
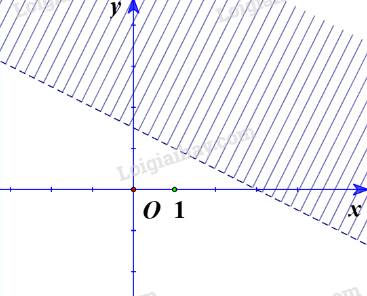
b) Ta vẽ đường thẳng d:\(3x - 4y = - 3 \Leftrightarrow y = \frac{{3x}}{4} + \frac{3}{4}\)
Thay tọa độ điểm O(0;0) vào bất phương trình \(3x - 4y \ge - 3\) ta được:
\(3.0 - 4.0 = 0 \ge - 3\) (Luôn đúng)
Vậy O nằm trong miền nghiệm.
Ta có miền nghiệm:
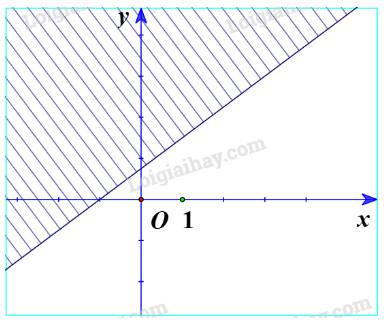
c) Ta vẽ đường thẳng d:\(y = - 2x + 4\)
Thay tọa độ điểm O(0;0) vào bất phương trình \(y \ge - 2x + 4\) ta được:
\(0 \ge - 2.0 + 4 \Leftrightarrow 0 \ge 4\) (Vô lí)
Vậy O không nằm trong miền nghiệm.
Ta có miền nghiệm:
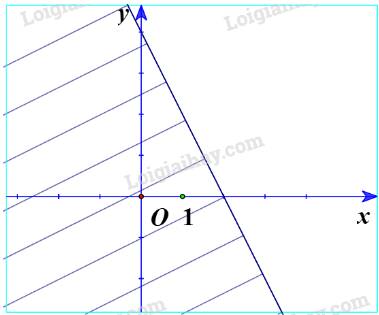
d) Ta vẽ đường thẳng d:\(y = 1 - 2x\)
Thay tọa độ điểm O(0;0) vào bất phương trình \(y < 1 - 2x\) ta được:
\(0 < 1 - 2.0\) (Luôn đúng)
Vậy O nằm trong miền nghiệm.
Ta có miền nghiệm:
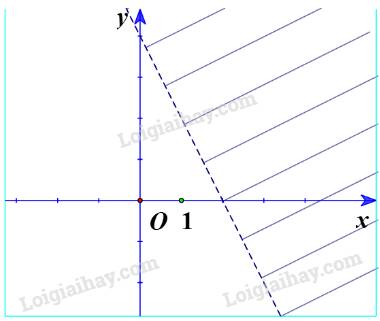
Chú ý
Đối với các bất phương trình có dấu “<” hoặc “>” thì vẽ đường thẳng là nét đứt.
Đối với các bất phương trình có dấu “\( \le \)” hoặc “\( \ge \)” thì vẽ đường thẳng là nét liền.
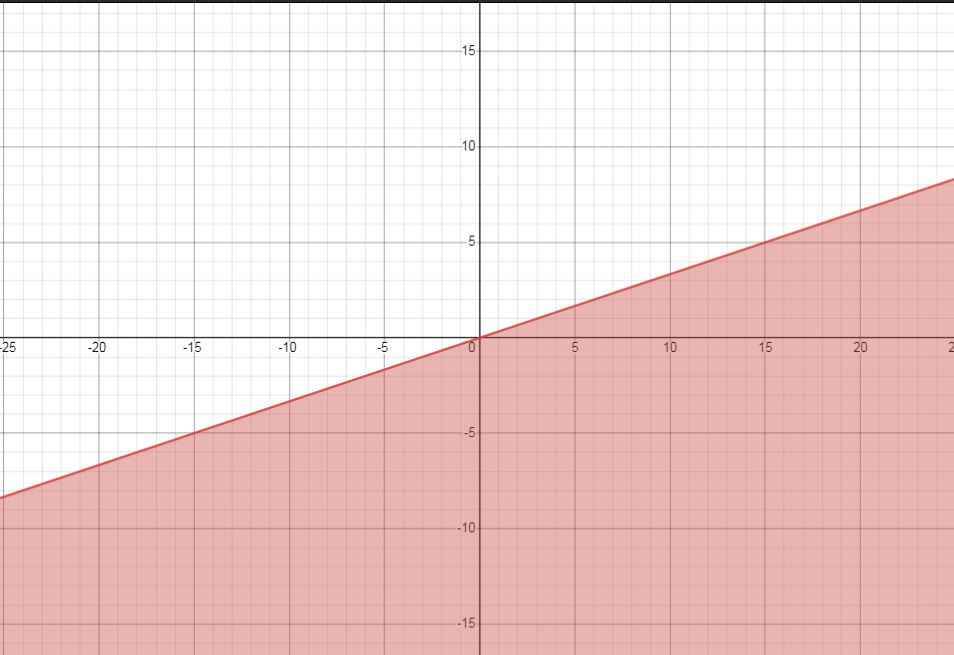

a) \(2x-y\ge0\)
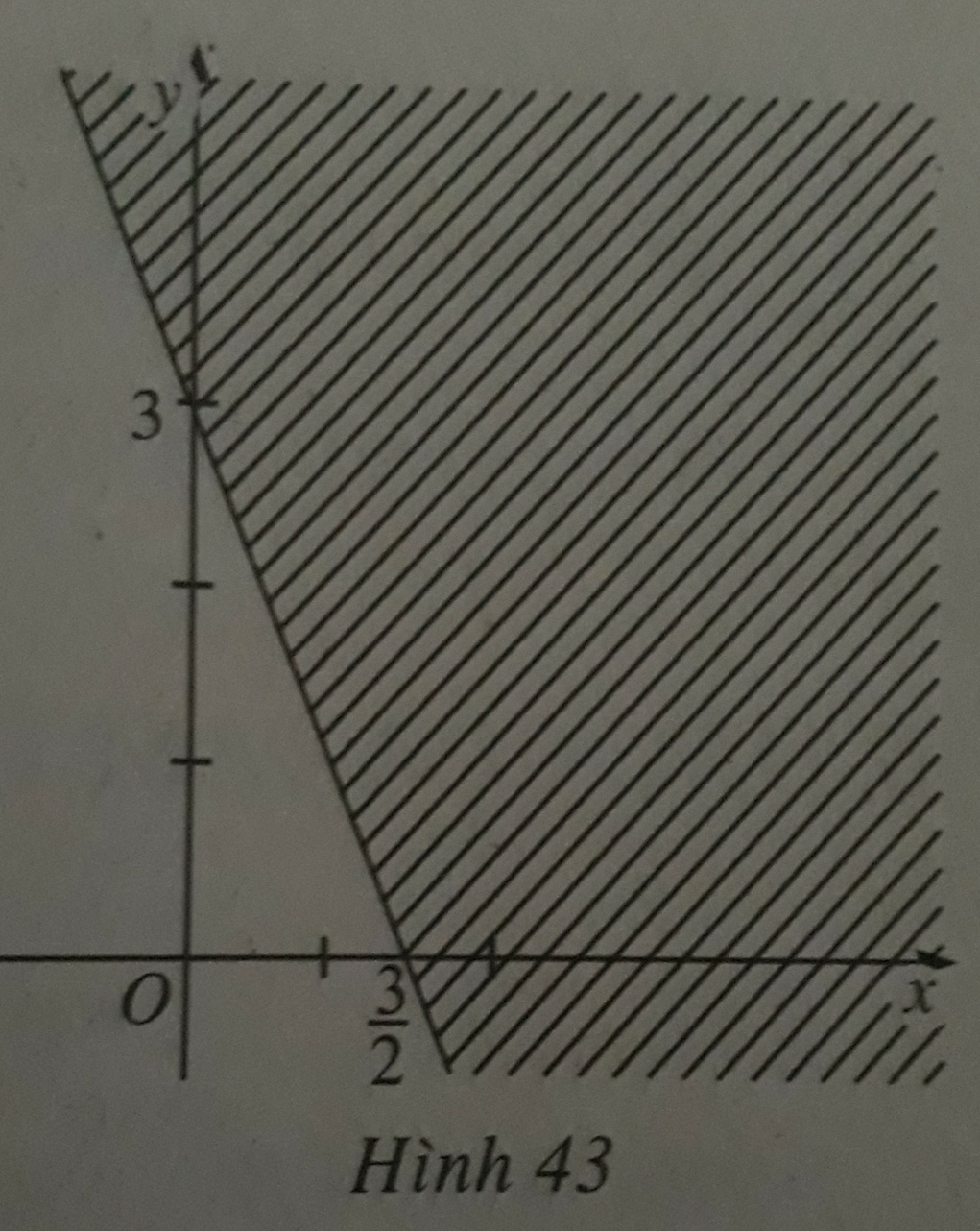
b) \(\dfrac{x-2y}{2}>\dfrac{2x+y+1}{3}\)
\(\Leftrightarrow3x-6y>4x+2y+1\)
\(\Leftrightarrow x+8y+1< 0\)