Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có y ' = x 2 - 4 x + 3 . Tiếp tuyến của đồ thị (C) song song với đường thẳng y = 3x - 1 nên hệ số góc của tiếp tuyến là k = 3.
Xét y' = 3 <=> x 2 - 4 x = 0
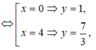
Phương trình tiếp tuyến của đồ thị tại A(0;1) có hệ số góc k = 3 là y = 3x + 1
Phương trình tiếp tuyến của đồ thị tại B(4; 7/3) có hệ số góc k = 3 là
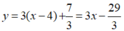
Chọn đáp án D.
Ta có \(y'=-4x^3-2x\)
a) Vì tiếp tuyến vuông góc với đường thẳng \(d:y=\frac{1}{6}x-\frac{1}{6}\)
Suy ra \(y'\left(x_0\right)=-6\Leftrightarrow2x_0^3+x_0^2-3=0\Leftrightarrow x_0=1\Rightarrow y_0=-3\)
Phương trình tiếp tuyến là \(y=-6x+3\)
b) Vì tuyến tuyến song song với đường thẳng \(y=6x+2\) nên ta có :
\(y'\left(x_0\right)=6\Leftrightarrow2x_0^3+x_0^2+3=0\Leftrightarrow\left(x_0+1\right)\left(2x_0^2-2x_0+3\right)=0\Rightarrow x_0=-1\Rightarrow y_0=-3\)
Nên ta có phương trình tiếp tuyến là :
\(y=6\left(x+1\right)-3=6x+3\)
2x mũ 3 cộng x ũ 2 cộng 3 bằng 0 là ban lấy ở đâu đó ạ mình không hiểu
Hàm số xác định với mọi \(x\ne1\). Ta có : \(y'=\frac{-4}{\left(x-1\right)^2}\)
Gọi \(M\left(x_0;y_0\right);\left(x_0\ne1\right)\) là tiếp điểm, suy ra phương trình tiếp tuyến của (C) :
\(\Delta:y=\frac{-4}{\left(x_0-1\right)^2}\left(x-x_0\right)+\frac{2x_0+2}{x_0-1}\)
a) Vì tiếp tuyến có hệ số góc bằng -4 nên ta có :
\(\frac{4}{\left(x_0-1\right)^2}=-16\Leftrightarrow\left[\begin{array}{nghiempt}x_0=\frac{3}{2}\\x_0=\frac{1}{2}\end{array}\right.\)
* \(x_0=\frac{3}{2}\Rightarrow y_0=10\Rightarrow\Delta=-16\left(x-\frac{3}{2}\right)+10\) hay \(y=-16x+22\)
* \(x_0=\frac{1}{2}\Rightarrow y_0=-6\Rightarrow\Delta=-16\left(x-\frac{1}{2}\right)-6\) hay \(y=-16x+2\)
b) Vì tiếp tuyến song song với đường thẳng d : \(y=-4x+1\) nên ta có :\(y'\left(x_0\right)=-4\Leftrightarrow\frac{-4}{\left(x_0-1\right)^2}=-4\Leftrightarrow x_0=0;x_0=2\)* \(x_0=0\Rightarrow y_0=2\Rightarrow\Delta:y=-4x+2\)* \(x_0=2\Rightarrow y_0=6\Rightarrow\Delta:y=-4x+14\) c) Vì tiếp tuyến tạo với 2 trục tọa độ 1 tam giác vuông cân nên tiếp tuyến phải vuông góc với một trong hai đường phân giác \(y=\pm x\), do đó hệ số góc của tiếp tuyến bằng \(\pm1\) hay \(y'\left(x_0\right)=\pm1\) mà \(y'>0\), mọi \(x\ne1\) nên ta có :\(y'\left(x_0\right)=-1\Leftrightarrow\frac{-4}{\left(x_0-1\right)^2}=-1\Leftrightarrow x_0=-1;x_0=3\)* \(x_0=-1\Rightarrow y_0=0\Rightarrow\Delta:y=-x-1\)* \(x_0=3\Rightarrow y_0=4\Rightarrow\Delta:y=-x+7\)
Giả sử tiếp điểm cần tìm có tọa độ ( x 0 ; y 0 ) thì f′( x 0 ) = 12 x 2 0 + 1 = 13 (vì tiếp tuyến song song với đường thẳng (d): y = 3x + 1). Từ đó ta có: x 0 = 1 hoặc x 0 = -1
Vậy có hai tiếp tuyến phải tìm là y = 13x + 8 hoặc y = 13x - 8
Ta có 
Gọi 
là một điểm thuộc đồ thị hàm số. Khi đó phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm M là:
Theo đề bài ta có đường thẳng 
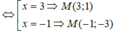
+) Phương trình tiếp tuyến của đồ thị hàm số tại 
là: 
(tm)
+) Phương trình tiếp tuyến của đồ thị hàm số tại 
là: 
( ktm do ≡ (d) )
Chọn B
Lời giải:
Ta có \(y=\frac{3x+6}{x-1}\Rightarrow y'=\frac{-9}{(x-1)^2}\)
Gọi tiếp điểm của tiếp tuyến với đồ thị C là \(M\left(x_0,\frac{3x_0+6}{x_0-1}\right)\)
PTTT: \(y=f'(x_0)(x-x_0)+f(x_0)\)
\(\Leftrightarrow y=\frac{-9}{(x_0-1)^2}(x-x_0)+\frac{3x_0+6}{x_0-1}=\frac{-9x}{(x_0-1)^2}+\frac{3x_0^2+12x_0-6}{(x_0-1)^2}\)
Để ĐT trên song song với \(d:3x+4y-21=0\) thì:
\(\frac{-9}{(x_0-1)^2}=\frac{-3}{4}\Leftrightarrow x_0=1\pm 2\sqrt{3}\)
Do đó PTTT là: \(y=\frac{-3x}{4}+\frac{15\pm 12\sqrt{3}}{4}\Leftrightarrow 3x+4y-(15\pm 12\sqrt{3})=0\)
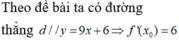
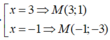
Tiếp tuyến có hệ số góc bằng −1/4.
Hoành độ tiếp điểm phải thỏa mãn phương trình
⇔ 2 x + 1 2 = 16
Hai tiếp tuyến cần tìm là