Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Diện tích xung quanh của hình chóp tam giác đều là: \(\frac{{10.3}}{2}.12 = 180\) (\(c{m^2}\))
b) Diện tích xung quanh của hình chóp tứ giác đều là: \(\frac{{72.4}}{2}.77 = 11088\) (\(d{m^2}\))
Diện tích đáy của hình chóp tứ giác đều là: \({72^2}=5184\) (\(d{m^2}\))
Diện tích toàn phần của hình chóp tứ giác đều là: \(11088 + 5184 = 16 272\) (\(d{m^2}\))
Thể tích của hình chóp tứ giác đều là: \(\frac{1}{3}.5184.68,1=117676,8\) (\(d{m^3}\))

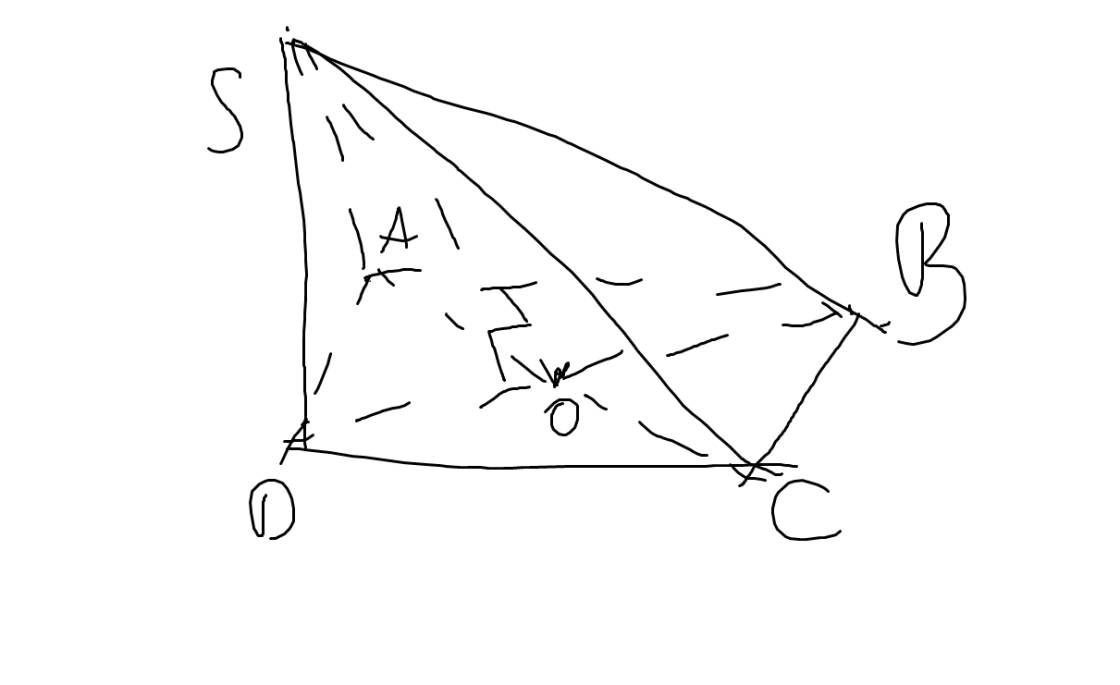
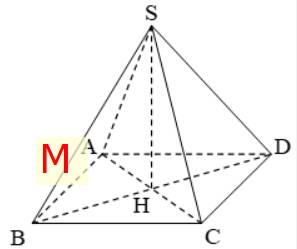
Trong hình chóp tứ giác đều, đường cao kẻ từ đỉnh xuống đáy có chân đường cao là tâm của đáy và đường cao đó chính là trung đoạn của hình chóp
a: Vẽ SO\(\perp\)(ABCD)
=>SO là trung đoạn của hình chóp ABCD và O là tâm của hình vuông ABCD
=>O là trung điểm chung của AC và BD
ABCD là hình vuông
=>\(AC=BD=\sqrt{4^2+4^2}=4\sqrt{2}\left(cm\right)\)
=>\(AO=BO=CO=DO=\dfrac{4\sqrt{2}}{2}=2\sqrt{2}\left(cm\right)\)
SO vuông góc (ABCD)
=>SO vuông góc OD
=>ΔSOD vuông tại O
=>\(SO^2+OD^2=SD^2\)
=>\(SO^2=6^2-8=28\)
=>\(SO=2\sqrt{7}\left(cm\right)\)
b: \(S_{Xq}=p\cdot d=C_{đáy}\cdot SO=4\cdot4\cdot2\sqrt{7}=32\sqrt{7}\left(cm^2\right)\)
c: \(S_{tp}=S_{xq}+S_{đáy}\)
\(=32\sqrt{7}+4^2=32\sqrt{7}+16\left(cm^2\right)\)

a)
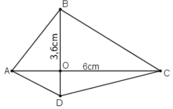
Có thể vẽ được vô số tứ giác theo yêu cầu từ đề bài. Chẳng hạn tứ giác ABCD ở hình trên.
Ta có: AC = 6cm, BD = 3,6cm và AC ⊥ BD.
Diện tích tứ giác ABCD là:
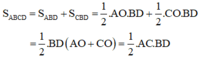
Mà AC = 6cm ; BD = 3,6 cm nên 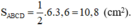
b) Hình vuông có 2 đường chéo vuông góc nên theo công thức trên, diện tích của nó là: 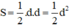

Sxq=16*4*17/2=544cm2
Stp=544+16^2=800cm2
V=1/3*16^2*15=1280cm3
Nữa chu vi đáy của hình chóp đều:
\(16\cdot4:2=32\left(cm\right)\)
Diện tích xung quanh của hình chóp đều:
\(S_{xq}=32\cdot17=544\left(cm^2\right)\)
Diện tích mặt đáy của hình chóp đều:
\(S_đ=16^2=256\left(cm^2\right)\)
Diện tích toàn phần của hình chóp đều:
\(S_{tp}=S_đ+S_{xq}=544+256=800\left(cm^2\right)\)
Thể tích của hình chóp đều:
\(V=\dfrac{1}{3}\cdot256\cdot15=1280\left(cm^3\right)\)

a)
Ta có: các mặt bên của hình chóp đều là những tam giác đều cạnh 5cm. Đường cao của mỗi mặt bên:

b)
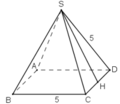
Mặt bên của hình chóp lục giác đều là tam giác cân có cạnh bên 10cm, cạnh đáy 6cm.

Diện tích toàn phần của hình chóp là:
Stp = Sxq + Sđ = 171,72 + 93,6 = 265,32(cm2)

Gọi M là trung điểm của AB:
\(\Rightarrow MA=MB=\dfrac{AB}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Do SM là ⊥ AB nên ΔSAM vuông tại M áp dụng định lý Py-ta-go ta có:
\(SA^2=SM^2+MA^2\)
\(\Rightarrow13^2=SM^2+5^2\)
\(\Rightarrow SM=\sqrt{13^2-5^2}=12\left(cm\right)\)
Nữa chu vi đáy của hình chóp tứ giác đều:
\(p=\dfrac{4\cdot10}{2}=20\left(cm\right)\)
Diện tích xung quanh của chóp tứ giác đều là:
\(S_{xq}=p\cdot d=20\cdot12=240\left(cm^2\right)\)
Ảnh tham khảo:
Gọi x (cm) là đường cao của mặt bên:
Ta có:
x² = 13² - 5² = 144
x = 12 (cm)
Diện tích xung quanh của hình chóp:
4 . 12 . 10 : 2 = 240 (cm²)
Dog
Cat